Håvard Rue
The Bayesian Learning Rule
Jul 09, 2021
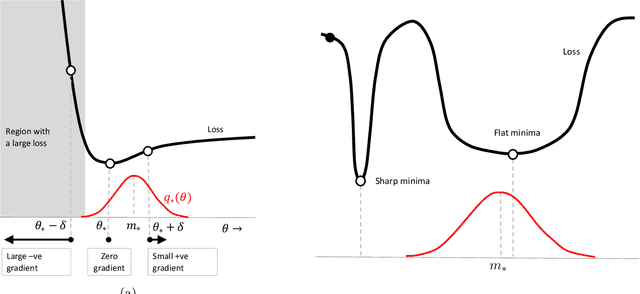
Abstract:We show that many machine-learning algorithms are specific instances of a single algorithm called the Bayesian learning rule. The rule, derived from Bayesian principles, yields a wide-range of algorithms from fields such as optimization, deep learning, and graphical models. This includes classical algorithms such as ridge regression, Newton's method, and Kalman filter, as well as modern deep-learning algorithms such as stochastic-gradient descent, RMSprop, and Dropout. The key idea in deriving such algorithms is to approximate the posterior using candidate distributions estimated by using natural gradients. Different candidate distributions result in different algorithms and further approximations to natural gradients give rise to variants of those algorithms. Our work not only unifies, generalizes, and improves existing algorithms, but also helps us design new ones.
Efficient Quantile Tracking Using an Oracle
Apr 27, 2020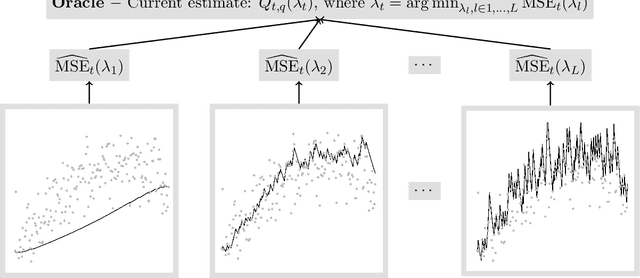
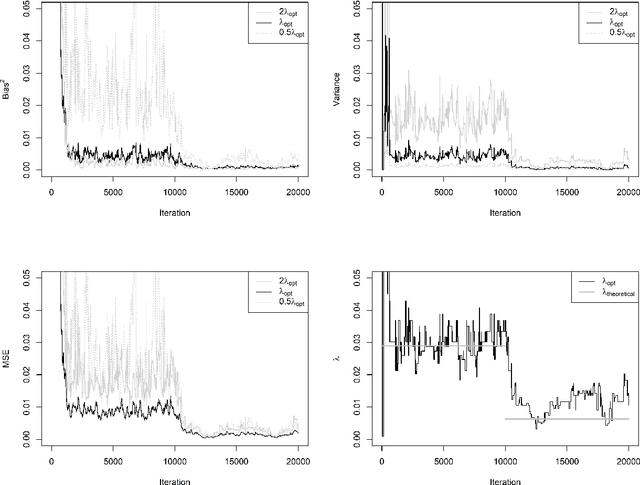
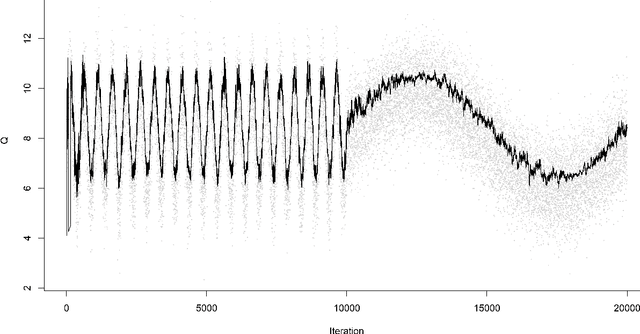
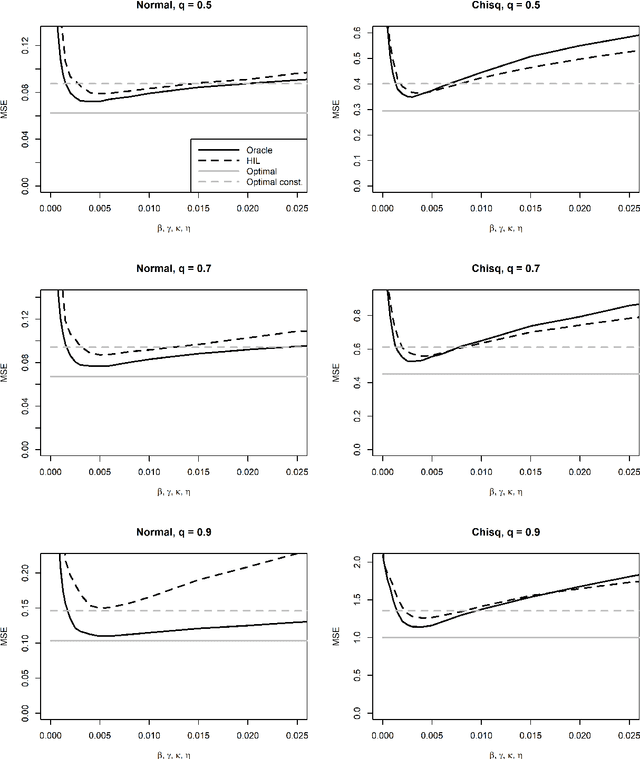
Abstract:For incremental quantile estimators the step size and possibly other tuning parameters must be carefully set. However, little attention has been given on how to set these values in an online manner. In this article we suggest two novel procedures that address this issue. The core part of the procedures is to estimate the current tracking mean squared error (MSE). The MSE is decomposed in tracking variance and bias and novel and efficient procedures to estimate these quantities are presented. It is shown that estimation bias can be tracked by associating it with the portion of observations below the quantile estimates. The first procedure runs an ensemble of $L$ quantile estimators for wide range of values of the tuning parameters and typically around $L = 100$. In each iteration an oracle selects the best estimate by the guidance of the estimated MSEs. The second method only runs an ensemble of $L = 3$ estimators and thus the values of the tuning parameters need from time to time to be adjusted for the running estimators. The procedures have a low memory foot print of $8L$ and a computational complexity of $8L$ per iteration. The experiments show that the procedures are highly efficient and track quantiles with an error close to the theoretical optimum. The Oracle approach performs best, but comes with higher computational cost. The procedures were further applied to a massive real-life data stream of tweets and proofed real world applicability of them.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge