Guoliang He
CuAsmRL: Optimizing GPU SASS Schedules via Deep Reinforcement Learning
Jan 14, 2025

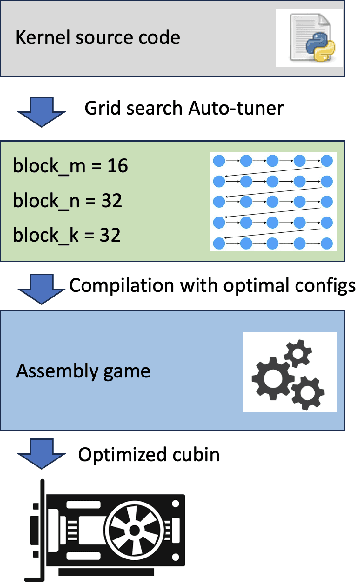

Abstract:Large language models (LLMs) are remarked by their substantial computational requirements. To mitigate the cost, researchers develop specialized CUDA kernels, which often fuse several tensor operations to maximize the utilization of GPUs as much as possible. However, those specialized kernels may still leave performance on the table as CUDA assembly experts show that manual optimization of GPU SASS schedules can lead to better performance, and trial-and-error is largely employed to manually find the best GPU SASS schedules. In this work, we employ an automatic approach to optimize GPU SASS schedules, which thus can be integrated into existing compiler frameworks. The key to automatic optimization is training an RL agent to mimic how human experts perform manual scheduling. To this end, we formulate an assembly game, where RL agents can play to find the best GPU SASS schedules. The assembly game starts from a \textit{-O3} optimized SASS schedule, and the RL agents can iteratively apply actions to mutate the current schedules. Positive rewards are generated if the mutated schedules get higher throughput by executing on GPUs. Experiments show that CuAsmRL can further improve the performance of existing specialized CUDA kernels transparently by up to $26\%$, and on average $9\%$. Moreover, it is used as a tool to reveal potential optimization moves learned automatically.
Safeguarding System Prompts for LLMs
Dec 18, 2024



Abstract:Large language models (LLMs) are increasingly utilized in applications where system prompts, which guide model outputs, play a crucial role. These prompts often contain business logic and sensitive information, making their protection essential. However, adversarial and even regular user queries can exploit LLM vulnerabilities to expose these hidden prompts. To address this issue, we present PromptKeeper, a novel defense mechanism for system prompt privacy. By reliably detecting worst-case leakage and regenerating outputs without the system prompt when necessary, PromptKeeper ensures robust protection against prompt extraction attacks via either adversarial or regular queries, while preserving conversational capability and runtime efficiency during benign user interactions.
Optimizing Tensor Computation Graphs with Equality Saturation and Monte Carlo Tree Search
Oct 07, 2024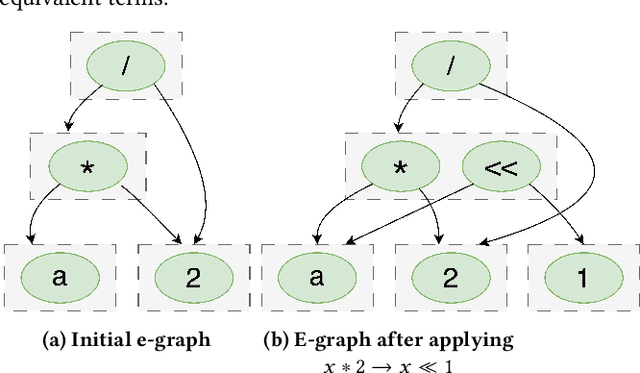

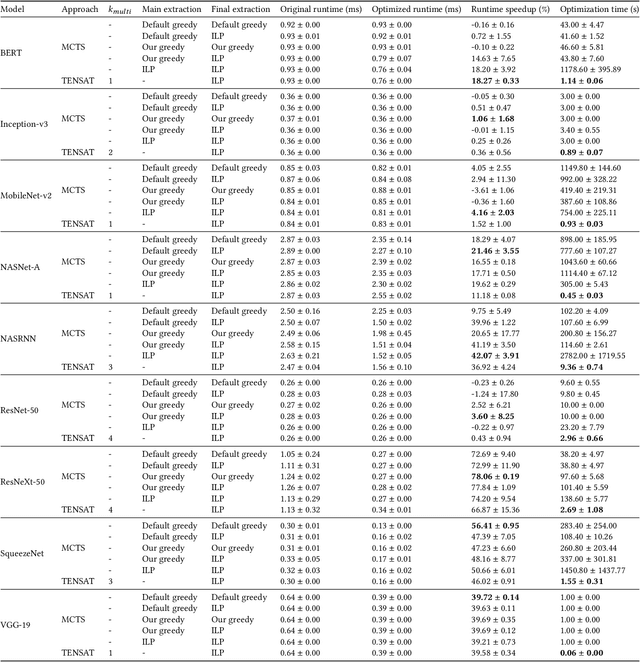
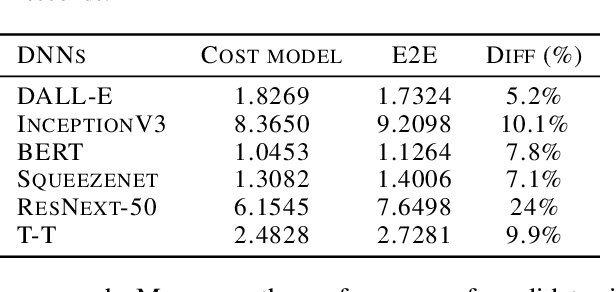
Abstract:The real-world effectiveness of deep neural networks often depends on their latency, thereby necessitating optimization techniques that can reduce a model's inference time while preserving its performance. One popular approach is to sequentially rewrite the input computation graph into an equivalent but faster one by replacing individual subgraphs. This approach gives rise to the so-called phase-ordering problem in which the application of one rewrite rule can eliminate the possibility to apply an even better one later on. Recent work has shown that equality saturation, a technique from compiler optimization, can mitigate this issue by first building an intermediate representation (IR) that efficiently stores multiple optimized versions of the input program before extracting the best solution in a second step. In practice, however, memory constraints prevent the IR from capturing all optimized versions and thus reintroduce the phase-ordering problem in the construction phase. In this paper, we present a tensor graph rewriting approach that uses Monte Carlo tree search to build superior IRs by identifying the most promising rewrite rules. We also introduce a novel extraction algorithm that can provide fast and accurate runtime estimates of tensor programs represented in an IR. Our approach improves the inference speedup of neural networks by up to 11% compared to existing methods.
SIP: Autotuning GPU Native Schedules via Stochastic Instruction Perturbation
Mar 25, 2024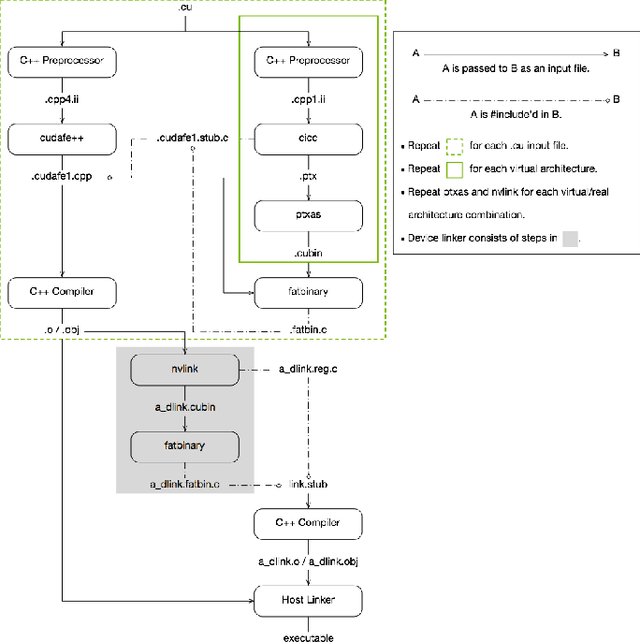
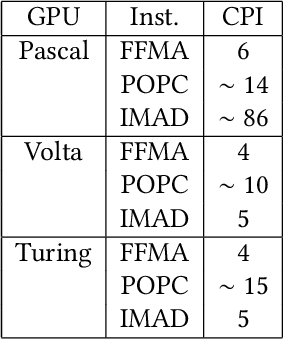
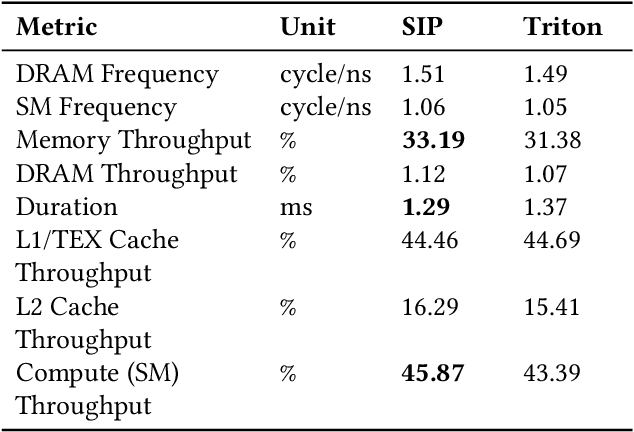
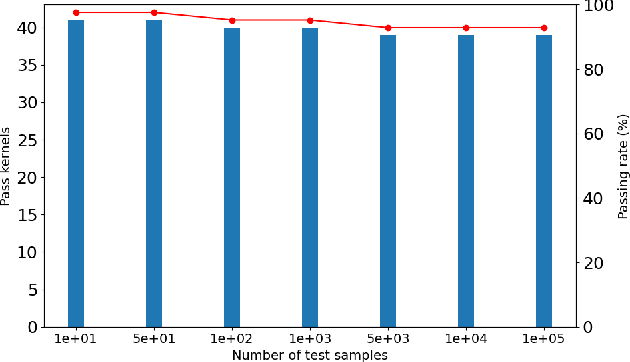
Abstract:Large language models (LLMs) have become a significant workload since their appearance. However, they are also computationally expensive as they have billions of parameters and are trained with massive amounts of data. Thus, recent works have developed dedicated CUDA kernels for LLM training and inference instead of relying on compilergenerated ones, so that hardware resources are as fully utilized as possible. In this work, we explore the possibility of GPU native instruction optimization to further push the CUDA kernels to extreme performance. Contrary to prior works, we adopt an automatic optimization approach by defining a search space of possible GPU native instruction schedules, and then we apply stochastic search to perform optimization. Experiments show that SIP can further improve CUDA kernel throughput by automatically discovering better GPU native instruction schedules and the optimized schedules are tested by 10 million test samples.
X-RLflow: Graph Reinforcement Learning for Neural Network Subgraphs Transformation
Apr 28, 2023
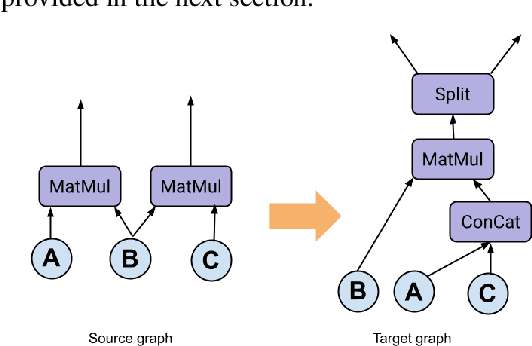
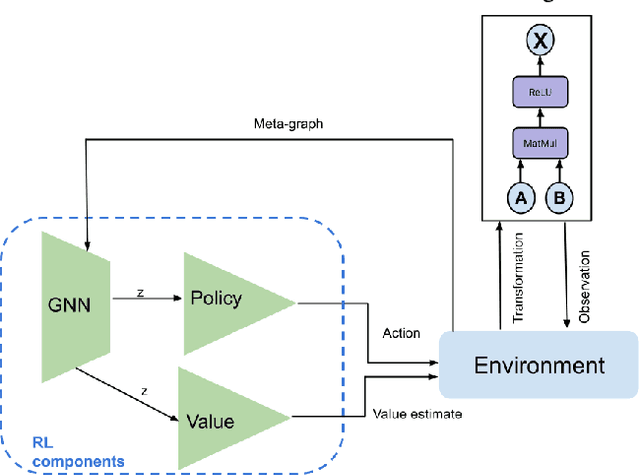
Abstract:Tensor graph superoptimisation systems perform a sequence of subgraph substitution to neural networks, to find the optimal computation graph structure. Such a graph transformation process naturally falls into the framework of sequential decision-making, and existing systems typically employ a greedy search approach, which cannot explore the whole search space as it cannot tolerate a temporary loss of performance. In this paper, we address the tensor graph superoptimisation problem by exploring an alternative search approach, reinforcement learning (RL). Our proposed approach, X-RLflow, can learn to perform neural network dataflow graph rewriting, which substitutes a subgraph one at a time. X-RLflow is based on a model-free RL agent that uses a graph neural network (GNN) to encode the target computation graph and outputs a transformed computation graph iteratively. We show that our approach can outperform state-of-the-art superoptimisation systems over a range of deep learning models and achieve by up to 40% on those that are based on transformer-style architectures.
MCTS-GEB: Monte Carlo Tree Search is a Good E-graph Builder
Mar 08, 2023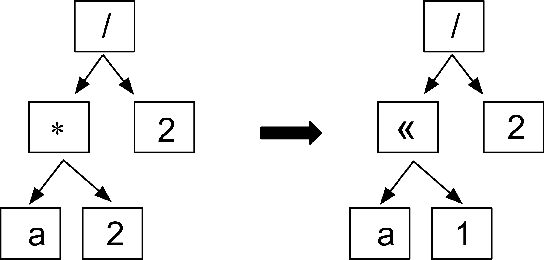
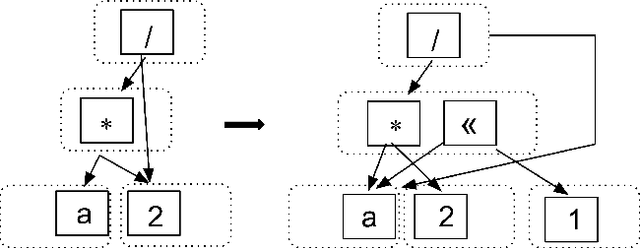
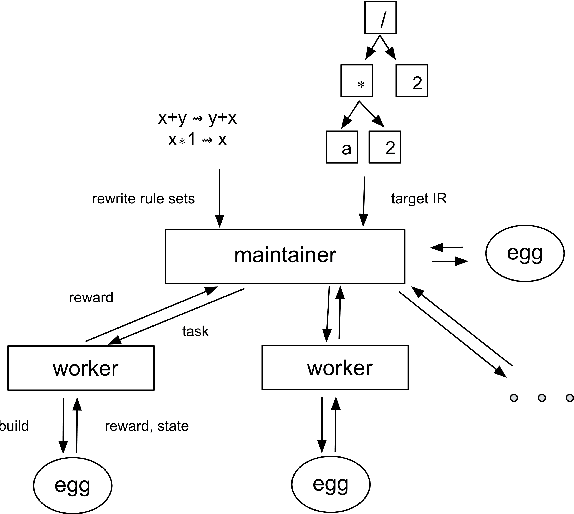
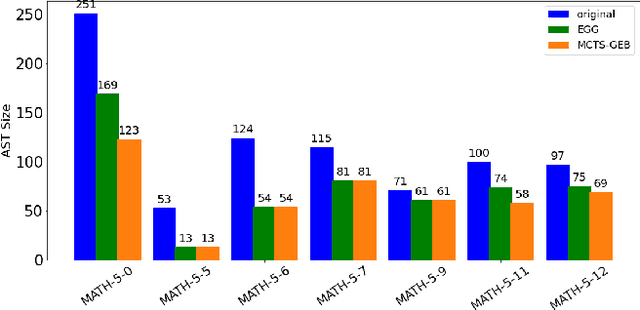
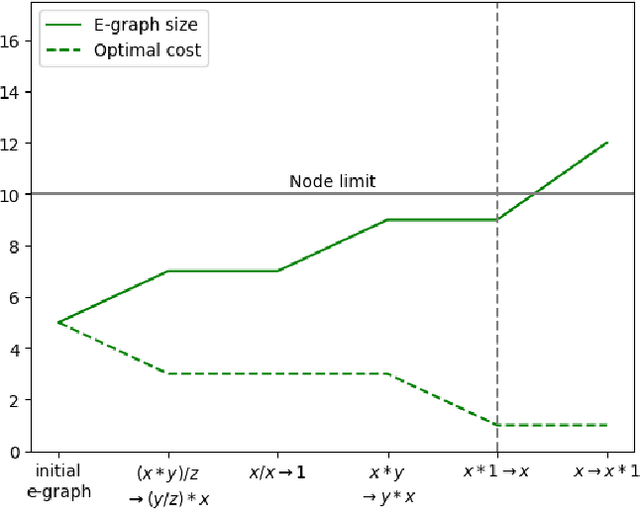
Abstract:Rewrite systems [6, 10, 12] have been widely employing equality saturation [9], which is an optimisation methodology that uses a saturated e-graph to represent all possible sequences of rewrite simultaneously, and then extracts the optimal one. As such, optimal results can be achieved by avoiding the phase-ordering problem. However, we observe that when the e-graph is not saturated, it cannot represent all possible rewrite opportunities and therefore the phase-ordering problem is re-introduced during the construction phase of the e-graph. To address this problem, we propose MCTS-GEB, a domain-general rewrite system that applies reinforcement learning (RL) to e-graph construction. At its core, MCTS-GEB uses a Monte Carlo Tree Search (MCTS) [3] to efficiently plan for the optimal e-graph construction, and therefore it can effectively eliminate the phase-ordering problem at the construction phase and achieve better performance within a reasonable time. Evaluation in two different domains shows MCTS-GEB can outperform the state-of-the-art rewrite systems by up to 49x, while the optimisation can generally take less than an hour, indicating MCTS-GEB is a promising building block for the future generation of rewrite systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge