Optimizing Tensor Computation Graphs with Equality Saturation and Monte Carlo Tree Search

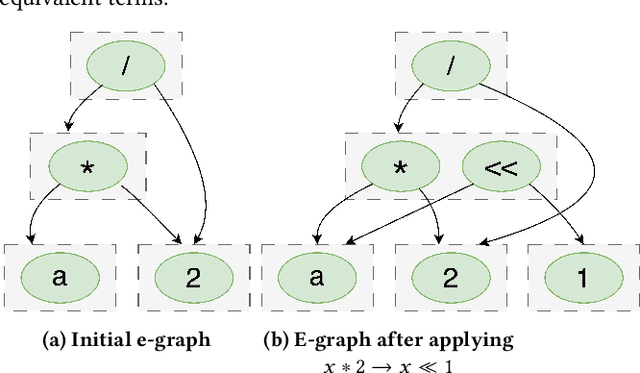
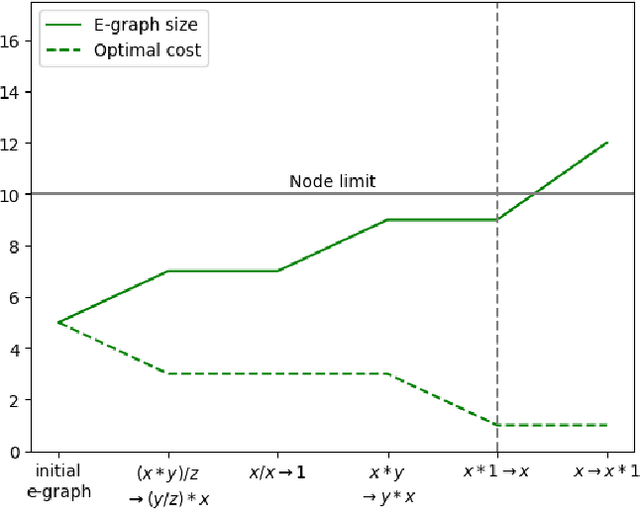
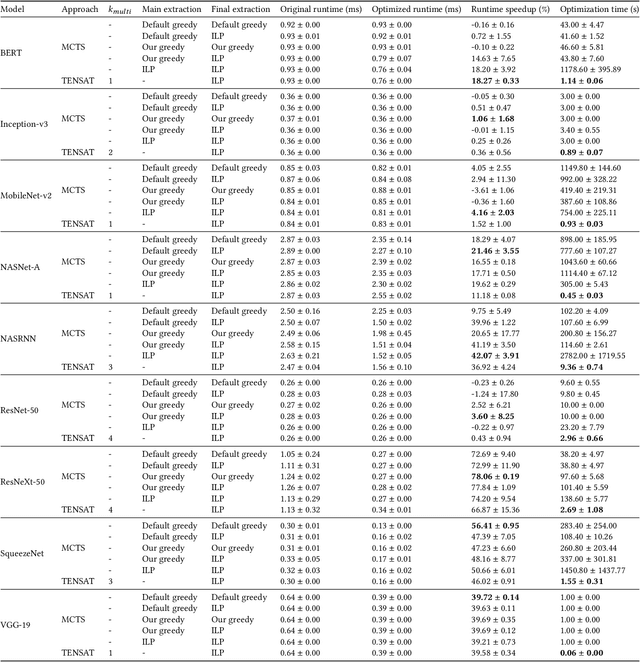
The real-world effectiveness of deep neural networks often depends on their latency, thereby necessitating optimization techniques that can reduce a model's inference time while preserving its performance. One popular approach is to sequentially rewrite the input computation graph into an equivalent but faster one by replacing individual subgraphs. This approach gives rise to the so-called phase-ordering problem in which the application of one rewrite rule can eliminate the possibility to apply an even better one later on. Recent work has shown that equality saturation, a technique from compiler optimization, can mitigate this issue by first building an intermediate representation (IR) that efficiently stores multiple optimized versions of the input program before extracting the best solution in a second step. In practice, however, memory constraints prevent the IR from capturing all optimized versions and thus reintroduce the phase-ordering problem in the construction phase. In this paper, we present a tensor graph rewriting approach that uses Monte Carlo tree search to build superior IRs by identifying the most promising rewrite rules. We also introduce a novel extraction algorithm that can provide fast and accurate runtime estimates of tensor programs represented in an IR. Our approach improves the inference speedup of neural networks by up to 11% compared to existing methods.