Segmenting Watermarked Texts From Language Models

Watermarking is a technique that involves embedding nearly unnoticeable statistical signals within generated content to help trace its source. This work focuses on a scenario where an untrusted third-party user sends prompts to a trusted language model (LLM) provider, who then generates a text from their LLM with a watermark. This setup makes it possible for a detector to later identify the source of the text if the user publishes it. The user can modify the generated text by substitutions, insertions, or deletions. Our objective is to develop a statistical method to detect if a published text is LLM-generated from the perspective of a detector. We further propose a methodology to segment the published text into watermarked and non-watermarked sub-strings. The proposed approach is built upon randomization tests and change point detection techniques. We demonstrate that our method ensures Type I and Type II error control and can accurately identify watermarked sub-strings by finding the corresponding change point locations. To validate our technique, we apply it to texts generated by several language models with prompts extracted from Google's C4 dataset and obtain encouraging numerical results. We release all code publicly at https://github.com/doccstat/llm-watermark-cpd.

Importance is Important: A Guide to Informed Importance Tempering Methods

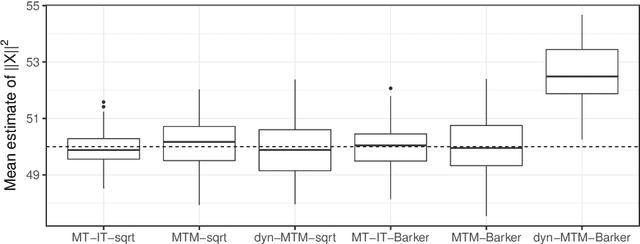
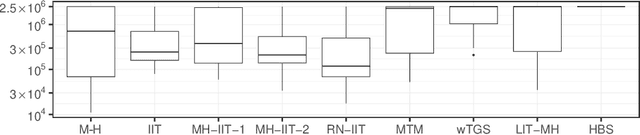
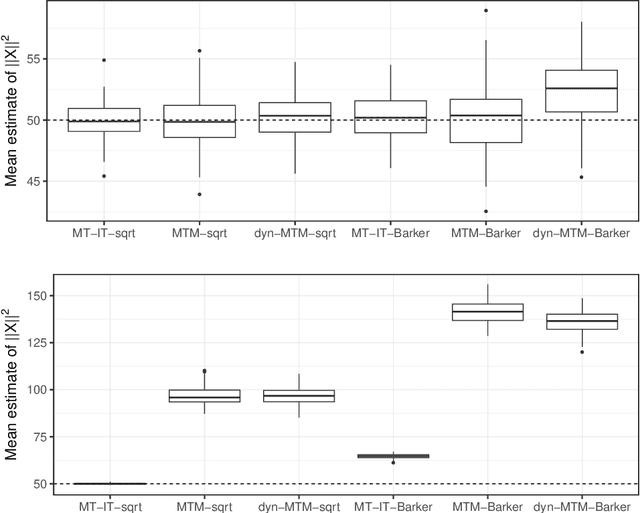
Informed importance tempering (IIT) is an easy-to-implement MCMC algorithm that can be seen as an extension of the familiar Metropolis-Hastings algorithm with the special feature that informed proposals are always accepted, and which was shown in Zhou and Smith (2022) to converge much more quickly in some common circumstances. This work develops a new, comprehensive guide to the use of IIT in many situations. First, we propose two IIT schemes that run faster than existing informed MCMC methods on discrete spaces by not requiring the posterior evaluation of all neighboring states. Second, we integrate IIT with other MCMC techniques, including simulated tempering, pseudo-marginal and multiple-try methods (on general state spaces), which have been conventionally implemented as Metropolis-Hastings schemes and can suffer from low acceptance rates. The use of IIT allows us to always accept proposals and brings about new opportunities for optimizing the sampler which are not possible under the Metropolis-Hastings framework. Numerical examples illustrating our findings are provided for each proposed algorithm, and a general theory on the complexity of IIT methods is developed.