Importance is Important: A Guide to Informed Importance Tempering Methods
Paper and Code
Apr 13, 2023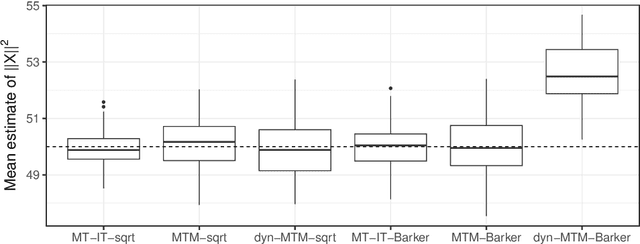

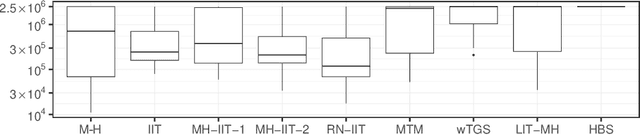
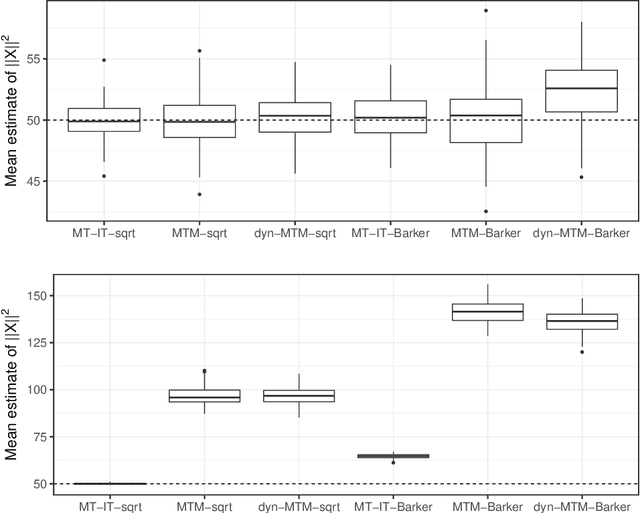
Informed importance tempering (IIT) is an easy-to-implement MCMC algorithm that can be seen as an extension of the familiar Metropolis-Hastings algorithm with the special feature that informed proposals are always accepted, and which was shown in Zhou and Smith (2022) to converge much more quickly in some common circumstances. This work develops a new, comprehensive guide to the use of IIT in many situations. First, we propose two IIT schemes that run faster than existing informed MCMC methods on discrete spaces by not requiring the posterior evaluation of all neighboring states. Second, we integrate IIT with other MCMC techniques, including simulated tempering, pseudo-marginal and multiple-try methods (on general state spaces), which have been conventionally implemented as Metropolis-Hastings schemes and can suffer from low acceptance rates. The use of IIT allows us to always accept proposals and brings about new opportunities for optimizing the sampler which are not possible under the Metropolis-Hastings framework. Numerical examples illustrating our findings are provided for each proposed algorithm, and a general theory on the complexity of IIT methods is developed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge