Neural Lithography: Close the Design-to-Manufacturing Gap in Computational Optics with a 'Real2Sim' Learned Photolithography Simulator

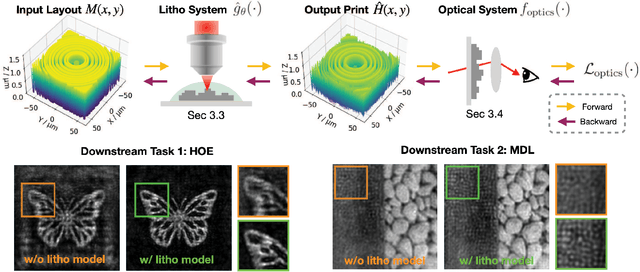
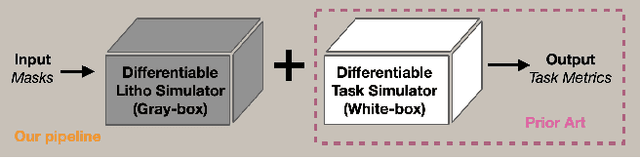
We introduce neural lithography to address the 'design-to-manufacturing' gap in computational optics. Computational optics with large design degrees of freedom enable advanced functionalities and performance beyond traditional optics. However, the existing design approaches often overlook the numerical modeling of the manufacturing process, which can result in significant performance deviation between the design and the fabricated optics. To bridge this gap, we, for the first time, propose a fully differentiable design framework that integrates a pre-trained photolithography simulator into the model-based optical design loop. Leveraging a blend of physics-informed modeling and data-driven training using experimentally collected datasets, our photolithography simulator serves as a regularizer on fabrication feasibility during design, compensating for structure discrepancies introduced in the lithography process. We demonstrate the effectiveness of our approach through two typical tasks in computational optics, where we design and fabricate a holographic optical element (HOE) and a multi-level diffractive lens (MDL) using a two-photon lithography system, showcasing improved optical performance on the task-specific metrics.

On the use of deep learning for phase recovery

Phase recovery (PR) refers to calculating the phase of the light field from its intensity measurements. As exemplified from quantitative phase imaging and coherent diffraction imaging to adaptive optics, PR is essential for reconstructing the refractive index distribution or topography of an object and correcting the aberration of an imaging system. In recent years, deep learning (DL), often implemented through deep neural networks, has provided unprecedented support for computational imaging, leading to more efficient solutions for various PR problems. In this review, we first briefly introduce conventional methods for PR. Then, we review how DL provides support for PR from the following three stages, namely, pre-processing, in-processing, and post-processing. We also review how DL is used in phase image processing. Finally, we summarize the work in DL for PR and outlook on how to better use DL to improve the reliability and efficiency in PR. Furthermore, we present a live-updating resource (https://github.com/kqwang/phase-recovery) for readers to learn more about PR.

High-performance real-world optical computing trained by in situ model-free optimization

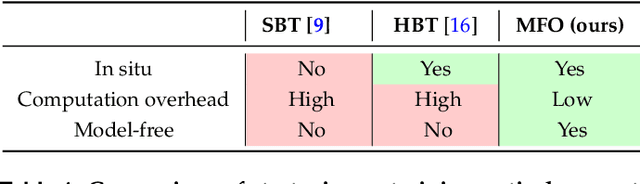
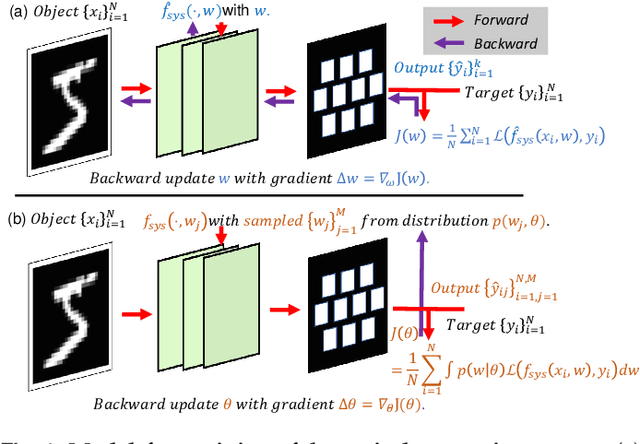
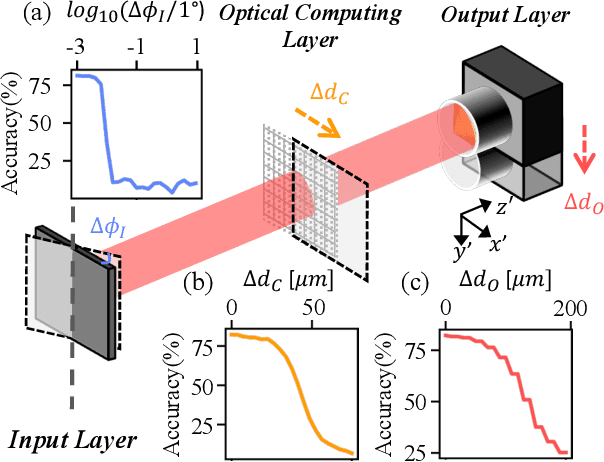
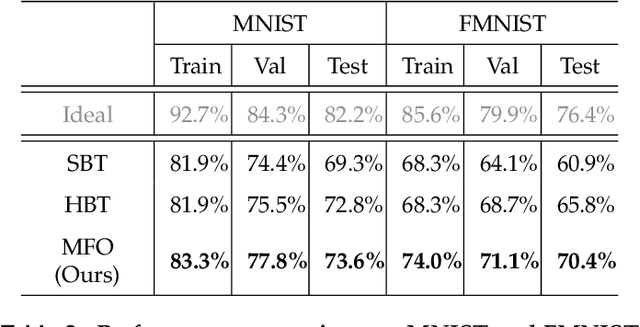
Optical computing systems can provide high-speed and low-energy data processing but face deficiencies in computationally demanding training and simulation-to-reality gap. We propose a model-free solution for lightweight in situ optimization of optical computing systems based on the score gradient estimation algorithm. This approach treats the system as a black box and back-propagates loss directly to the optical weights' probabilistic distributions, hence circumventing the need for computation-heavy and biased system simulation. We demonstrate a superior classification accuracy on the MNIST and FMNIST datasets through experiments on a single-layer diffractive optical computing system. Furthermore, we show its potential for image-free and high-speed cell analysis. The inherent simplicity of our proposed method, combined with its low demand for computational resources, expedites the transition of optical computing from laboratory demonstrations to real-world applications.

Blending Diverse Physical Priors with Neural Networks

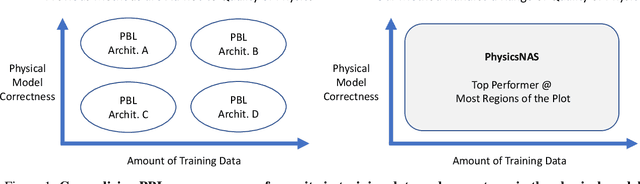
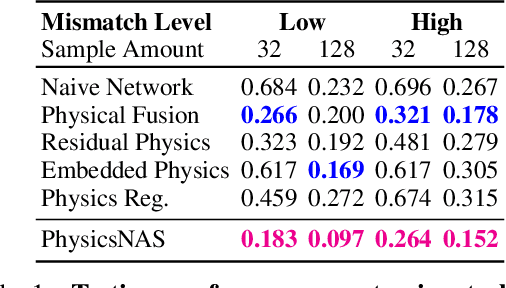
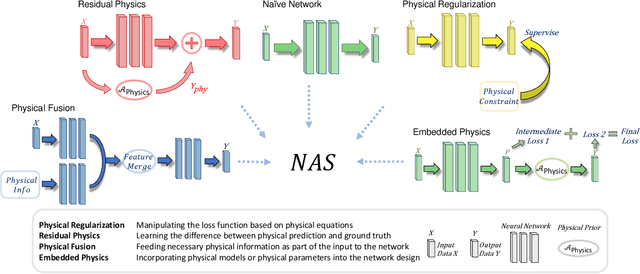
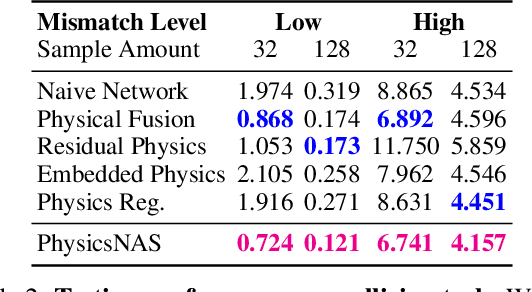
Machine learning in context of physical systems merits a re-examination of the learning strategy. In addition to data, one can leverage a vast library of physical prior models (e.g. kinematics, fluid flow, etc) to perform more robust inference. The nascent sub-field of \emph{physics-based learning} (PBL) studies the blending of neural networks with physical priors. While previous PBL algorithms have been applied successfully to specific tasks, it is hard to generalize existing PBL methods to a wide range of physics-based problems. Such generalization would require an architecture that can adapt to variations in the correctness of the physics, or in the quality of training data. No such architecture exists. In this paper, we aim to generalize PBL, by making a first attempt to bring neural architecture search (NAS) to the realm of PBL. We introduce a new method known as physics-based neural architecture search (PhysicsNAS) that is a top-performer across a diverse range of quality in the physical model and the dataset.