F-SE-LSTM: A Time Series Anomaly Detection Method with Frequency Domain Information

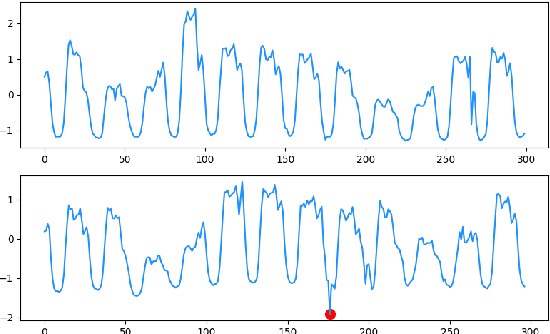
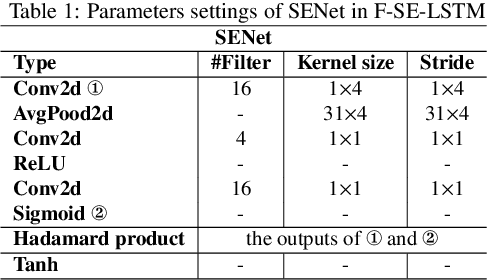
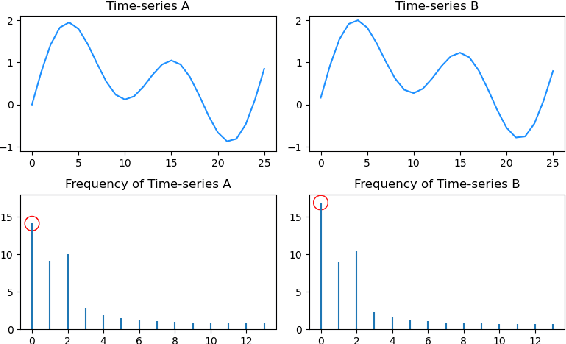
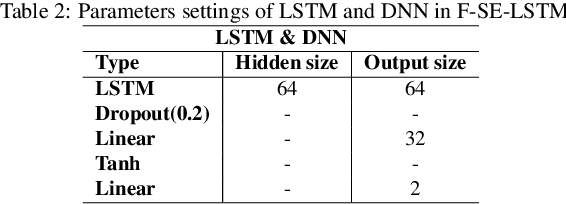
With the development of society, time series anomaly detection plays an important role in network and IoT services. However, most existing anomaly detection methods directly analyze time series in the time domain and cannot distinguish some relatively hidden anomaly sequences. We attempt to analyze the impact of frequency on time series from a frequency domain perspective, thus proposing a new time series anomaly detection method called F-SE-LSTM. This method utilizes two sliding windows and fast Fourier transform (FFT) to construct a frequency matrix. Simultaneously, Squeeze-and-Excitation Networks (SENet) and Long Short-Term Memory (LSTM) are employed to extract frequency-related features within and between periods. Through comparative experiments on multiple datasets such as Yahoo Webscope S5 and Numenta Anomaly Benchmark, the results demonstrate that the frequency matrix constructed by F-SE-LSTM exhibits better discriminative ability than ordinary time domain and frequency domain data. Furthermore, F-SE-LSTM outperforms existing state-of-the-art deep learning anomaly detection methods in terms of anomaly detection capability and execution efficiency.

Stochastic Conjugate Gradient Algorithm with Variance Reduction

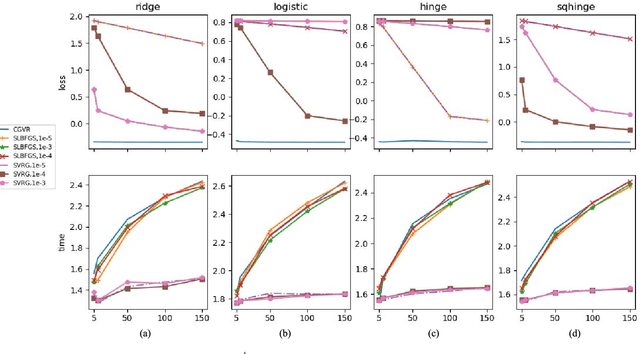
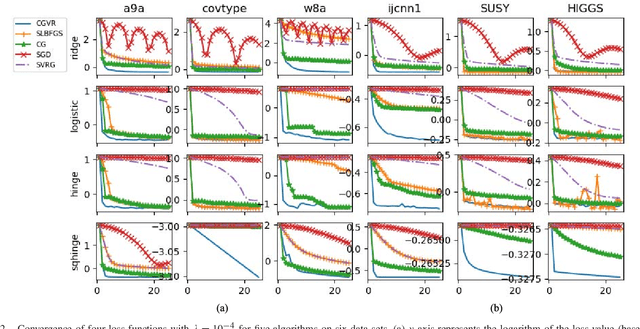
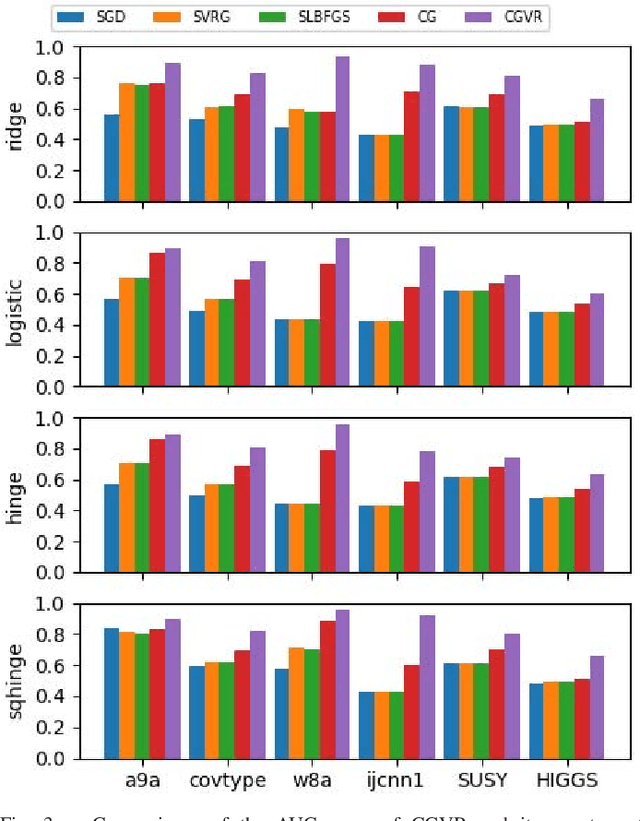
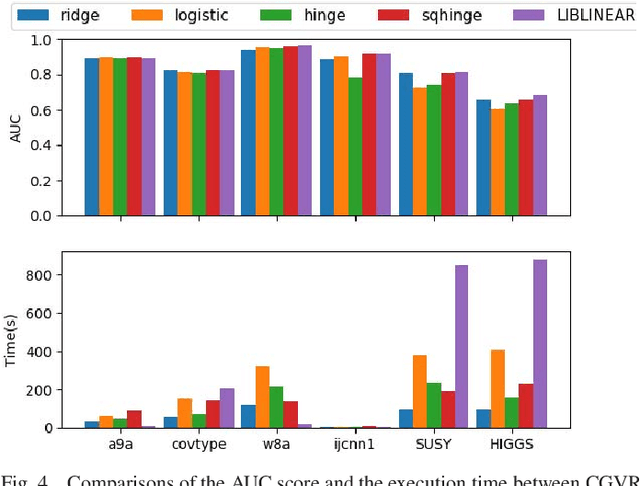
Conjugate gradient (CG) methods are a class of important methods for solving linear equations and nonlinear optimization problems. In this paper, we propose a new stochastic CG algorithm with variance reduction and we prove its linear convergence with the Fletcher and Reeves method for strongly convex and smooth functions. We experimentally demonstrate that the CG with variance reduction algorithm converges faster than its counterparts for four learning models, which may be convex, nonconvex or nonsmooth. In addition, its area under the curve performance on six large-scale data sets is comparable to that of the LIBLINEAR solver for the L2-regularized L2-loss but with a significant improvement in computational efficiency

Linear NDCG and Pair-wise Loss

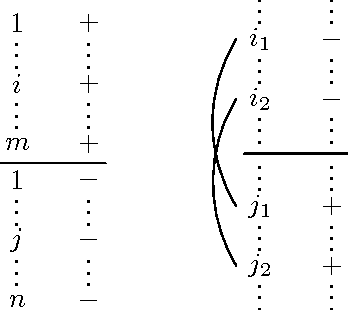
Linear NDCG is used for measuring the performance of the Web content quality assessment in ECML/PKDD Discovery Challenge 2010. In this paper, we will prove that the DCG error equals a new pair-wise loss.