Grzegorz Kwasniewski
Motif Prediction with Graph Neural Networks
Jun 05, 2021


Abstract:Link prediction is one of the central problems in graph mining. However, recent studies highlight the importance of higher-order network analysis, where complex structures called motifs are the first-class citizens. We first show that existing link prediction schemes fail to effectively predict motifs. To alleviate this, we establish a general motif prediction problem and we propose several heuristics that assess the chances for a specified motif to appear. To make the scores realistic, our heuristics consider - among others - correlations between links, i.e., the potential impact of some arriving links on the appearance of other links in a given motif. Finally, for highest accuracy, we develop a graph neural network (GNN) architecture for motif prediction. Our architecture offers vertex features and sampling schemes that capture the rich structural properties of motifs. While our heuristics are fast and do not need any training, GNNs ensure highest accuracy of predicting motifs, both for dense (e.g., k-cliques) and for sparse ones (e.g., k-stars). We consistently outperform the best available competitor by more than 10% on average and up to 32% in area under the curve. Importantly, the advantages of our approach over schemes based on uncorrelated link prediction increase with the increasing motif size and complexity. We also successfully apply our architecture for predicting more arbitrary clusters and communities, illustrating its potential for graph mining beyond motif analysis.
GraphMineSuite: Enabling High-Performance and Programmable Graph Mining Algorithms with Set Algebra
Mar 05, 2021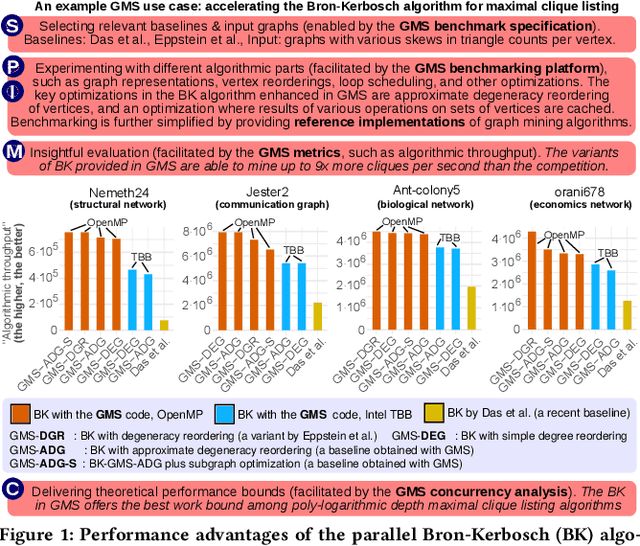

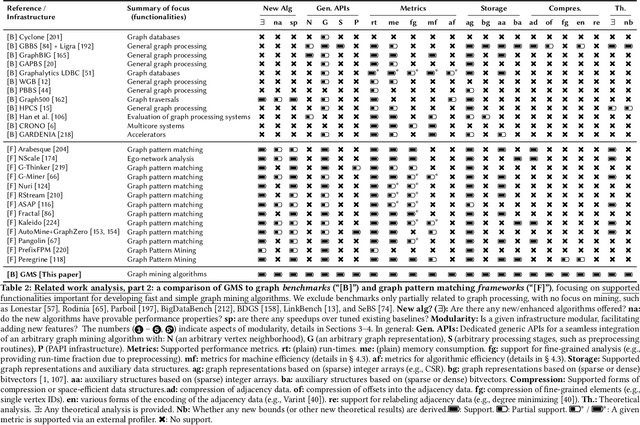

Abstract:We propose GraphMineSuite (GMS): the first benchmarking suite for graph mining that facilitates evaluating and constructing high-performance graph mining algorithms. First, GMS comes with a benchmark specification based on extensive literature review, prescribing representative problems, algorithms, and datasets. Second, GMS offers a carefully designed software platform for seamless testing of different fine-grained elements of graph mining algorithms, such as graph representations or algorithm subroutines. The platform includes parallel implementations of more than 40 considered baselines, and it facilitates developing complex and fast mining algorithms. High modularity is possible by harnessing set algebra operations such as set intersection and difference, which enables breaking complex graph mining algorithms into simple building blocks that can be separately experimented with. GMS is supported with a broad concurrency analysis for portability in performance insights, and a novel performance metric to assess the throughput of graph mining algorithms, enabling more insightful evaluation. As use cases, we harness GMS to rapidly redesign and accelerate state-of-the-art baselines of core graph mining problems: degeneracy reordering (by up to >2x), maximal clique listing (by up to >9x), k-clique listing (by 1.1x), and subgraph isomorphism (by up to 2.5x), also obtaining better theoretical performance bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge