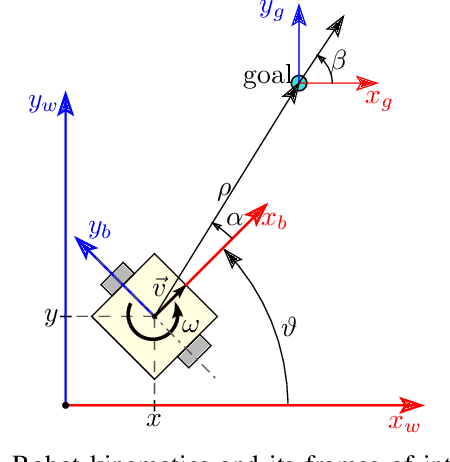
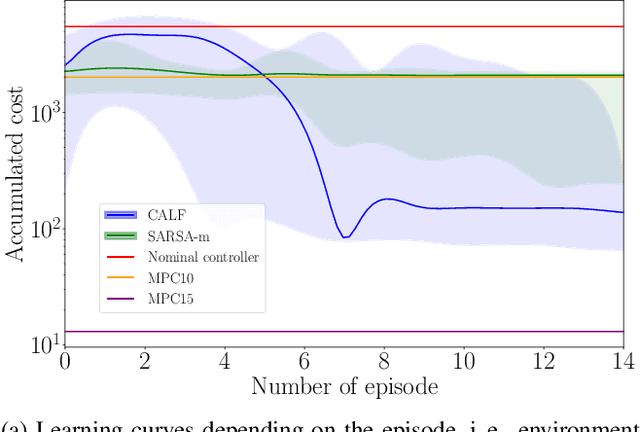
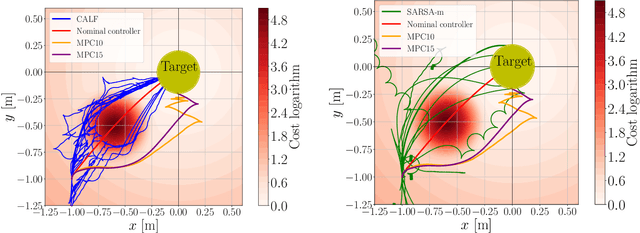
Critic as Lyapunov function (CALF): a model-free, stability-ensuring agent

This work presents and showcases a novel reinforcement learning agent called Critic As Lyapunov Function (CALF) which is model-free and ensures online environment, in other words, dynamical system stabilization. Online means that in each learning episode, the said environment is stabilized. This, as demonstrated in a case study with a mobile robot simulator, greatly improves the overall learning performance. The base actor-critic scheme of CALF is analogous to SARSA. The latter did not show any success in reaching the target in our studies. However, a modified version thereof, called SARSA-m here, did succeed in some learning scenarios. Still, CALF greatly outperformed the said approach. CALF was also demonstrated to improve a nominal stabilizer provided to it. In summary, the presented agent may be considered a viable approach to fusing classical control with reinforcement learning. Its concurrent approaches are mostly either offline or model-based, like, for instance, those that fuse model-predictive control into the agent.

An approach to improve agent learning via guaranteeing goal reaching in all episodes

Reinforcement learning is commonly concerned with problems of maximizing accumulated rewards in Markov decision processes. Oftentimes, a certain goal state or a subset of the state space attain maximal reward. In such a case, the environment may be considered solved when the goal is reached. Whereas numerous techniques, learning or non-learning based, exist for solving environments, doing so optimally is the biggest challenge. Say, one may choose a reward rate which penalizes the action effort. Reinforcement learning is currently among the most actively developed frameworks for solving environments optimally by virtue of maximizing accumulated reward, in other words, returns. Yet, tuning agents is a notoriously hard task as reported in a series of works. Our aim here is to help the agent learn a near-optimal policy efficiently while ensuring a goal reaching property of some basis policy that merely solves the environment. We suggest an algorithm, which is fairly flexible, and can be used to augment practically any agent as long as it comprises of a critic. A formal proof of a goal reaching property is provided. Simulation experiments on six problems under five agents, including the benchmarked one, provided an empirical evidence that the learning can indeed be boosted while ensuring goal reaching property.

On stabilizing reinforcement learning without Lyapunov functions

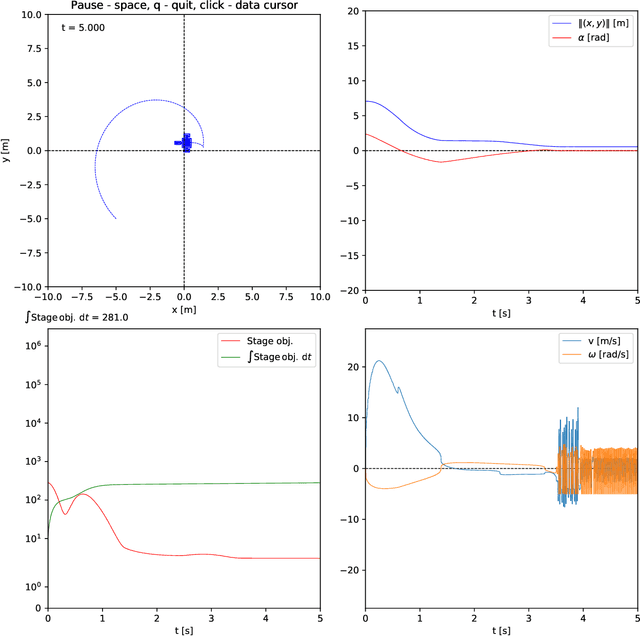
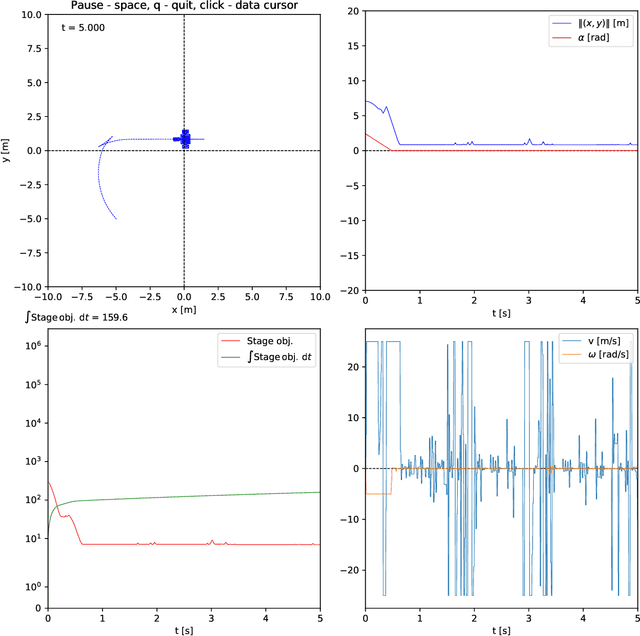
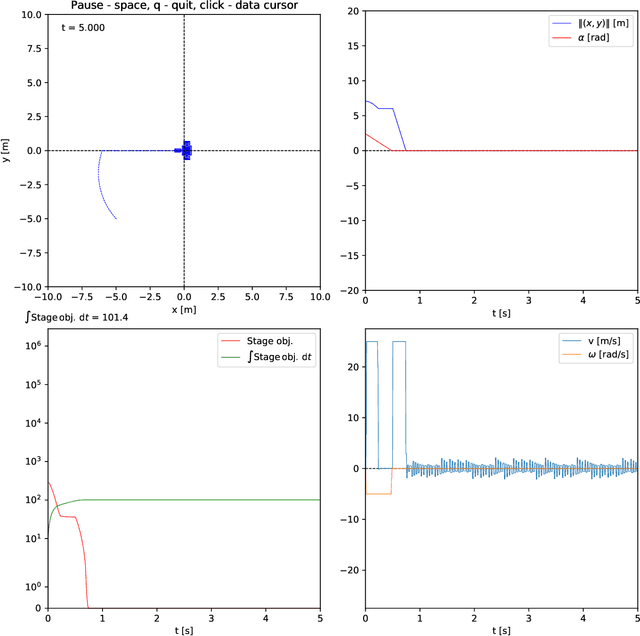
Reinforcement learning remains one of the major directions of the contemporary development of control engineering and machine learning. Nice intuition, flexible settings, ease of application are among the many perks of this methodology. From the standpoint of machine learning, the main strength of a reinforcement learning agent is its ability to ``capture" (learn) the optimal behavior in the given environment. Typically, the agent is built on neural networks and it is their approximation abilities that give rise to the above belief. From the standpoint of control engineering, however, reinforcement learning has serious deficiencies. The most significant one is the lack of stability guarantee of the agent-environment closed loop. A great deal of research was and is being made towards stabilizing reinforcement learning. Speaking of stability, the celebrated Lyapunov theory is the de facto tool. It is thus no wonder that so many techniques of stabilizing reinforcement learning rely on the Lyapunov theory in one way or another. In control theory, there is an intricate connection between a stabilizing controller and a Lyapunov function. Employing such a pair seems thus quite attractive to design stabilizing reinforcement learning. However, computation of a Lyapunov function is generally a cumbersome process. In this note, we show how to construct a stabilizing reinforcement learning agent that does not employ such a function at all. We only assume that a Lyapunov function exists, which is a natural thing to do if the given system (read: environment) is stabilizable, but we do not need to compute one.

On stochastic stabilization via non-smooth control Lyapunov functions

Control Lyapunov function is a central tool in stabilization. It generalizes an abstract energy function -- a Lyapunov function -- to the case of controlled systems. It is a known fact that most control Lyapunov functions are non-smooth -- so is the case in non-holonomic systems, like wheeled robots and cars. Frameworks for stabilization using non-smooth control Lyapunov functions exist, like Dini aiming and steepest descent. This work generalizes the related results to the stochastic case. As the groundwork, sampled control scheme is chosen in which control actions are computed at discrete moments in time using discrete measurements of the system state. In such a setup, special attention should be paid to the sample-to-sample behavior of the control Lyapunov function. A particular challenge here is a random noise acting on the system. The central result of this work is a theorem that states, roughly, that if there is a, generally non-smooth, control Lyapunov function, the given stochastic dynamical system can be practically stabilized in the sample-and-hold mode meaning that the control actions are held constant within sampling time steps. A particular control method chosen is based on Moreau-Yosida regularization, in other words, inf-convolution of the control Lyapunov function, but the overall framework is extendable to further control schemes. It is assumed that the system noise be bounded almost surely, although the case of unbounded noise is briefly addressed.

A comment on stabilizing reinforcement learning

This is a short comment on the paper "Asymptotically Stable Adaptive-Optimal Control Algorithm With Saturating Actuators and Relaxed Persistence of Excitation" by Vamvoudakis et al. The question of stability of reinforcement learning (RL) agents remains hard and the said work suggested an on-policy approach with a suitable stability property using a technique from adaptive control - a robustifying term to be added to the action. However, there is an issue with this approach to stabilizing RL, which we will explain in this note. Furthermore, Vamvoudakis et al. seems to have made a fallacious assumption on the Hamiltonian under a generic policy. To provide a positive result, we will not only indicate this mistake, but show critic neural network weight convergence under a stochastic, continuous-time environment, provided certain conditions on the behavior policy hold.