Grace Lai-Hung Wong
AUTOSHAPE: An Autoencoder-Shapelet Approach for Time Series Clustering
Aug 06, 2022



Abstract:Time series shapelets are discriminative subsequences that have been recently found effective for time series clustering (TSC). The shapelets are convenient for interpreting the clusters. Thus, the main challenge for TSC is to discover high-quality variable-length shapelets to discriminate different clusters. In this paper, we propose a novel autoencoder-shapelet approach (AUTOSHAPE), which is the first study to take the advantage of both autoencoder and shapelet for determining shapelets in an unsupervised manner. An autoencoder is specially designed to learn high-quality shapelets. More specifically, for guiding the latent representation learning, we employ the latest self-supervised loss to learn the unified embeddings for variable-length shapelet candidates (time series subsequences) of different variables, and propose the diversity loss to select the discriminating embeddings in the unified space. We introduce the reconstruction loss to recover shapelets in the original time series space for clustering. Finally, we adopt Davies Bouldin index (DBI) to inform AUTOSHAPE of the clustering performance during learning. We present extensive experiments on AUTOSHAPE. To evaluate the clustering performance on univariate time series (UTS), we compare AUTOSHAPE with 15 representative methods using UCR archive datasets. To study the performance of multivariate time series (MTS), we evaluate AUTOSHAPE on 30 UEA archive datasets with 5 competitive methods. The results validate that AUTOSHAPE is the best among all the methods compared. We interpret clusters with shapelets, and can obtain interesting intuitions about clusters in three UTS case studies and one MTS case study, respectively.
Temporal Matrix Completion with Locally Linear Latent Factors for Medical Applications
Oct 31, 2016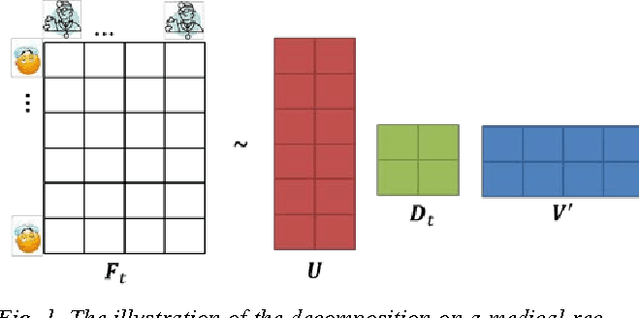
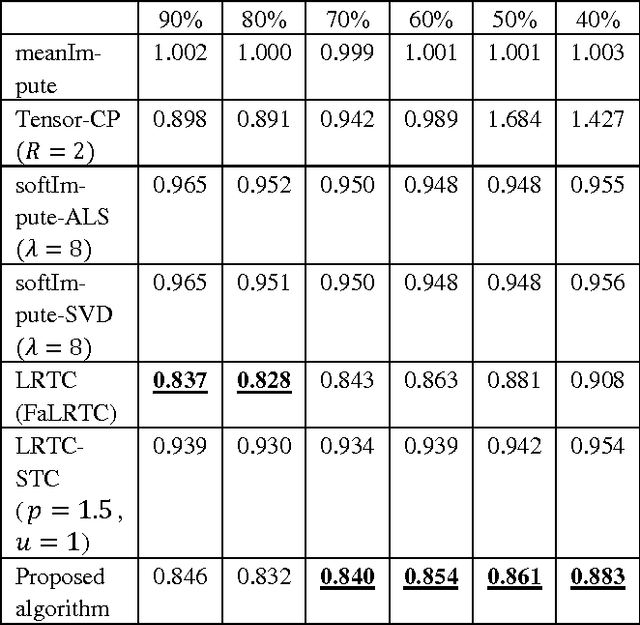
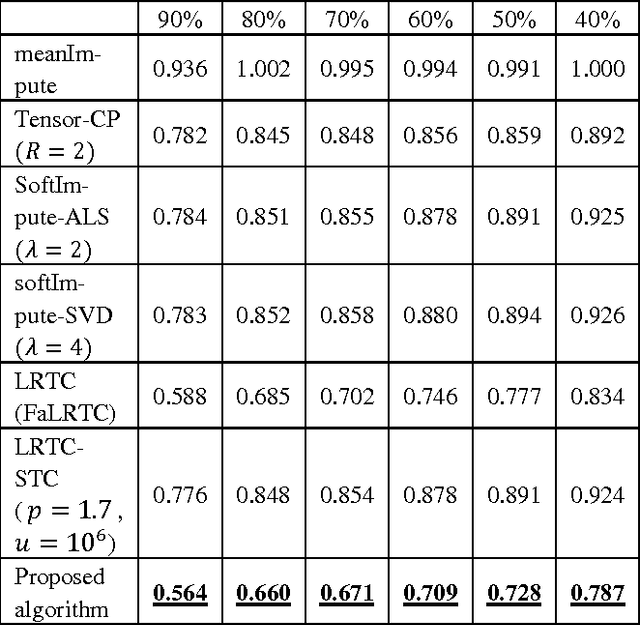
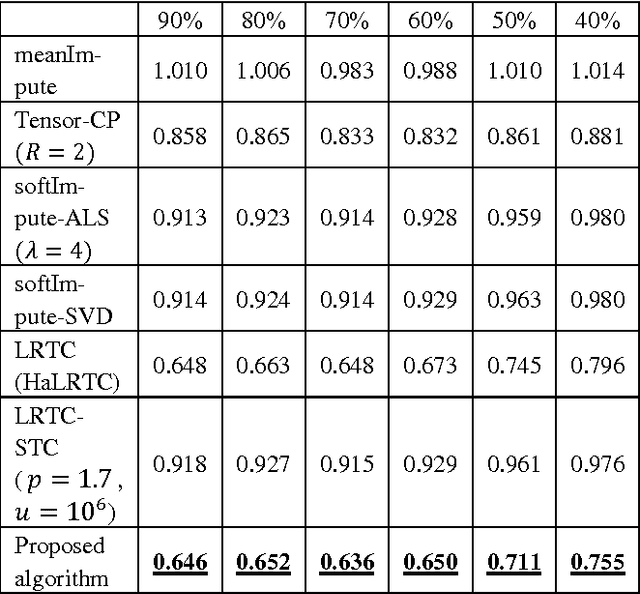
Abstract:Regular medical records are useful for medical practitioners to analyze and monitor patient health status especially for those with chronic disease, but such records are usually incomplete due to unpunctuality and absence of patients. In order to resolve the missing data problem over time, tensor-based model is suggested for missing data imputation in recent papers because this approach makes use of low rank tensor assumption for highly correlated data. However, when the time intervals between records are long, the data correlation is not high along temporal direction and such assumption is not valid. To address this problem, we propose to decompose a matrix with missing data into its latent factors. Then, the locally linear constraint is imposed on these factors for matrix completion in this paper. By using a publicly available dataset and two medical datasets collected from hospital, experimental results show that the proposed algorithm achieves the best performance by comparing with the existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge