Byron Choi
VSFormer: Value and Shape-Aware Transformer with Prior-Enhanced Self-Attention for Multivariate Time Series Classification
Dec 21, 2024Abstract:Multivariate time series classification is a crucial task in data mining, attracting growing research interest due to its broad applications. While many existing methods focus on discovering discriminative patterns in time series, real-world data does not always present such patterns, and sometimes raw numerical values can also serve as discriminative features. Additionally, the recent success of Transformer models has inspired many studies. However, when applying to time series classification, the self-attention mechanisms in Transformer models could introduce classification-irrelevant features, thereby compromising accuracy. To address these challenges, we propose a novel method, VSFormer, that incorporates both discriminative patterns (shape) and numerical information (value). In addition, we extract class-specific prior information derived from supervised information to enrich the positional encoding and provide classification-oriented self-attention learning, thereby enhancing its effectiveness. Extensive experiments on all 30 UEA archived datasets demonstrate the superior performance of our method compared to SOTA models. Through ablation studies, we demonstrate the effectiveness of the improved encoding layer and the proposed self-attention mechanism. Finally, We provide a case study on a real-world time series dataset without discriminative patterns to interpret our model.
AUTOSHAPE: An Autoencoder-Shapelet Approach for Time Series Clustering
Aug 06, 2022



Abstract:Time series shapelets are discriminative subsequences that have been recently found effective for time series clustering (TSC). The shapelets are convenient for interpreting the clusters. Thus, the main challenge for TSC is to discover high-quality variable-length shapelets to discriminate different clusters. In this paper, we propose a novel autoencoder-shapelet approach (AUTOSHAPE), which is the first study to take the advantage of both autoencoder and shapelet for determining shapelets in an unsupervised manner. An autoencoder is specially designed to learn high-quality shapelets. More specifically, for guiding the latent representation learning, we employ the latest self-supervised loss to learn the unified embeddings for variable-length shapelet candidates (time series subsequences) of different variables, and propose the diversity loss to select the discriminating embeddings in the unified space. We introduce the reconstruction loss to recover shapelets in the original time series space for clustering. Finally, we adopt Davies Bouldin index (DBI) to inform AUTOSHAPE of the clustering performance during learning. We present extensive experiments on AUTOSHAPE. To evaluate the clustering performance on univariate time series (UTS), we compare AUTOSHAPE with 15 representative methods using UCR archive datasets. To study the performance of multivariate time series (MTS), we evaluate AUTOSHAPE on 30 UEA archive datasets with 5 competitive methods. The results validate that AUTOSHAPE is the best among all the methods compared. We interpret clusters with shapelets, and can obtain interesting intuitions about clusters in three UTS case studies and one MTS case study, respectively.
Graph Embedding for Combinatorial Optimization: A Survey
Aug 26, 2020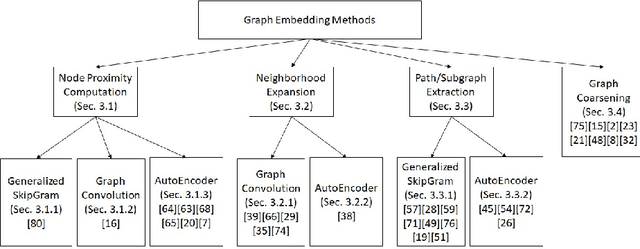
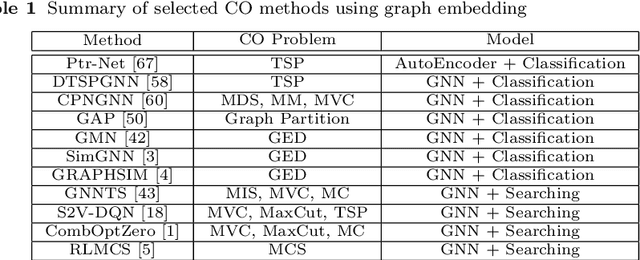


Abstract:Graphs have been widely used to represent complex data in many applications, such as e-commerce, social networks, and bioinformatics. Efficient and effective analysis of graph data is important for graph-based applications. However, most graph analysis tasks are combinatorial optimization (CO) problems, which are NP-hard. Recent studies have focused a lot on the potential of using machine learning (ML) to solve graph-based CO problems. Using ML- based CO methods, a graph has to be represented in numerical vectors, which is known as graph embedding. In this survey, we provide a thorough overview of recent graph embedding methods that have been used to solve CO problems. Most graph embedding methods have two stages: graph preprocessing and ML model learning. This survey classifies graph embedding works from the perspective of graph preprocessing tasks and ML models. Furthermore, this survey summarizes recent graph-based CO methods that exploit graph embedding. In particular, graph embedding can be employed as part of classification techniques or can be combined with search methods to find solutions to CO problems. The survey ends with several remarks on future research directions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge