Transport Gaussian Processes for Regression

Gaussian process (GP) priors are non-parametric generative models with appealing modelling properties for Bayesian inference: they can model non-linear relationships through noisy observations, have closed-form expressions for training and inference, and are governed by interpretable hyperparameters. However, GP models rely on Gaussianity, an assumption that does not hold in several real-world scenarios, e.g., when observations are bounded or have extreme-value dependencies, a natural phenomenon in physics, finance and social sciences. Although beyond-Gaussian stochastic processes have caught the attention of the GP community, a principled definition and rigorous treatment is still lacking. In this regard, we propose a methodology to construct stochastic processes, which include GPs, warped GPs, Student-t processes and several others under a single unified approach. We also provide formulas and algorithms for training and inference of the proposed models in the regression problem. Our approach is inspired by layers-based models, where each proposed layer changes a specific property over the generated stochastic process. That, in turn, allows us to push-forward a standard Gaussian white noise prior towards other more expressive stochastic processes, for which marginals and copulas need not be Gaussian, while retaining the appealing properties of GPs. We validate the proposed model through experiments with real-world data.

Compositionally-Warped Gaussian Processes

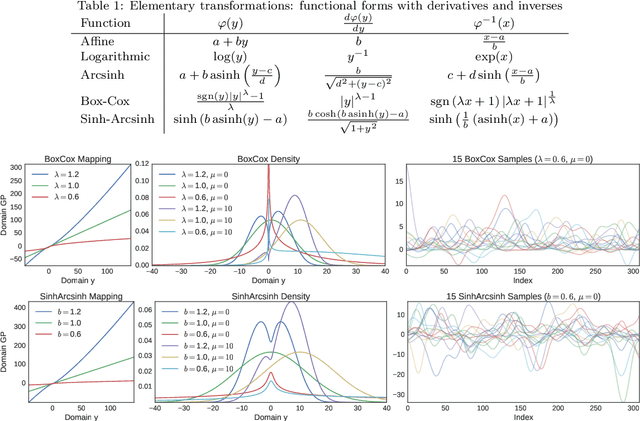
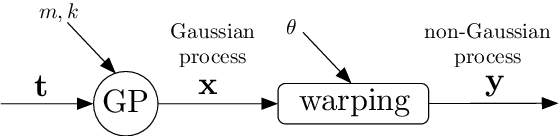
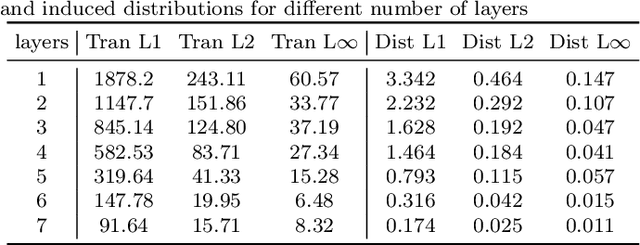
The Gaussian process (GP) is a nonparametric prior distribution over functions indexed by time, space, or other high-dimensional index set. The GP is a flexible model yet its limitation is given by its very nature: it can only model Gaussian marginal distributions. To model non-Gaussian data, a GP can be warped by a nonlinear transformation (or warping) as performed by warped GPs (WGPs) and more computationally-demanding alternatives such as Bayesian WGPs and deep GPs. However, the WGP requires a numerical approximation of the inverse warping for prediction, which increases the computational complexity in practice. To sidestep this issue, we construct a novel class of warpings consisting of compositions of multiple elementary functions, for which the inverse is known explicitly. We then propose the compositionally-warped GP (CWGP), a non-Gaussian generative model whose expressiveness follows from its deep compositional architecture, and its computational efficiency is guaranteed by the analytical inverse warping. Experimental validation using synthetic and real-world datasets confirms that the proposed CWGP is robust to the choice of warpings and provides more accurate point predictions, better trained models and shorter computation times than WGP.

Bayesian Learning with Wasserstein Barycenters

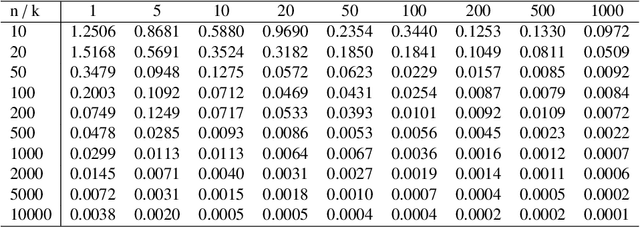
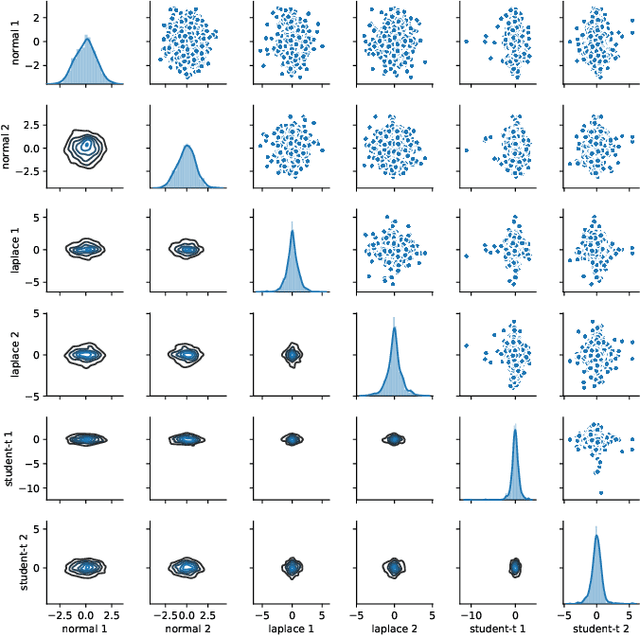
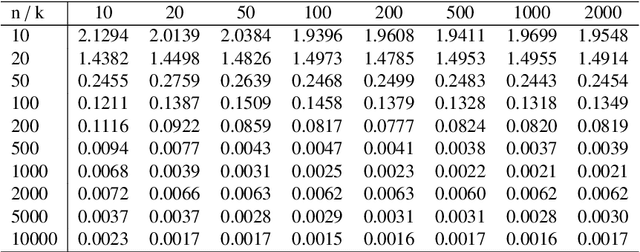
In this work we introduce a novel paradigm for Bayesian learning based on optimal transport theory. Namely, we propose to use the Wasserstein barycenter of the posterior law on models, as an alternative to the maximum a posteriori estimator and Bayesian model average. We exhibit conditions granting the existence and consistency of this estimator, discuss some of its basic and specific properties, and provide insight for practical implementations relying on standard sampling in finite-dimensional parameter spaces. We thus contribute to the recent blooming of applications of optimal transport theory in machine learning, beyond the discrete setting so far considered. The advantages of the proposed estimator are presented in theoretical terms and through analytical and numeral examples.

Learning non-Gaussian Time Series using the Box-Cox Gaussian Process

Gaussian processes (GPs) are Bayesian nonparametric generative models that provide interpretability of hyperparameters, admit closed-form expressions for training and inference, and are able to accurately represent uncertainty. To model general non-Gaussian data with complex correlation structure, GPs can be paired with an expressive covariance kernel and then fed into a nonlinear transformation (or warping). However, overparametrising the kernel and the warping is known to, respectively, hinder gradient-based training and make the predictions computationally expensive. We remedy this issue by (i) training the model using derivative-free global-optimisation techniques so as to find meaningful maxima of the model likelihood, and (ii) proposing a warping function based on the celebrated Box-Cox transformation that requires minimal numerical approximations---unlike existing warped GP models. We validate the proposed approach by first showing that predictions can be computed analytically, and then on a learning, reconstruction and forecasting experiment using real-world datasets.

Recovering Latent Signals from a Mixture of Measurements using a Gaussian Process Prior

In sensing applications, sensors cannot always measure the latent quantity of interest at the required resolution, sometimes they can only acquire a blurred version of it due the sensor's transfer function. To recover latent signals when only noisy mixed measurements of the signal are available, we propose the Gaussian process mixture of measurements (GPMM), which models the latent signal as a Gaussian process (GP) and allows us to perform Bayesian inference on such signal conditional to a set of noisy mixture of measurements. We describe how to train GPMM, that is, to find the hyperparameters of the GP and the mixing weights, and how to perform inference on the latent signal under GPMM; additionally, we identify the solution to the underdetermined linear system resulting from a sensing application as a particular case of GPMM. The proposed model is validated in the recovery of three signals: a smooth synthetic signal, a real-world heart-rate time series and a step function, where GPMM outperformed the standard GP in terms of estimation error, uncertainty representation and recovery of the spectral content of the latent signal.