Compositionally-Warped Gaussian Processes
Paper and Code
Jul 12, 2019
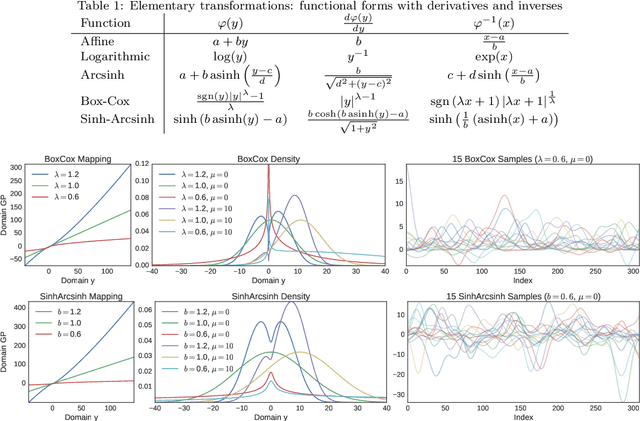
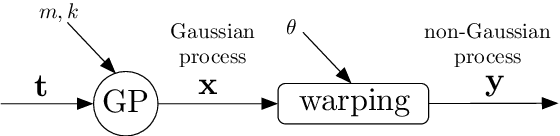
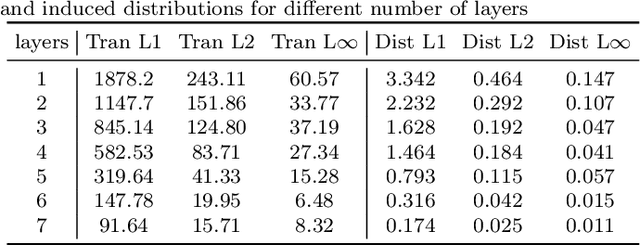
The Gaussian process (GP) is a nonparametric prior distribution over functions indexed by time, space, or other high-dimensional index set. The GP is a flexible model yet its limitation is given by its very nature: it can only model Gaussian marginal distributions. To model non-Gaussian data, a GP can be warped by a nonlinear transformation (or warping) as performed by warped GPs (WGPs) and more computationally-demanding alternatives such as Bayesian WGPs and deep GPs. However, the WGP requires a numerical approximation of the inverse warping for prediction, which increases the computational complexity in practice. To sidestep this issue, we construct a novel class of warpings consisting of compositions of multiple elementary functions, for which the inverse is known explicitly. We then propose the compositionally-warped GP (CWGP), a non-Gaussian generative model whose expressiveness follows from its deep compositional architecture, and its computational efficiency is guaranteed by the analytical inverse warping. Experimental validation using synthetic and real-world datasets confirms that the proposed CWGP is robust to the choice of warpings and provides more accurate point predictions, better trained models and shorter computation times than WGP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge