Bayesian Learning with Wasserstein Barycenters
Paper and Code
Jun 25, 2018
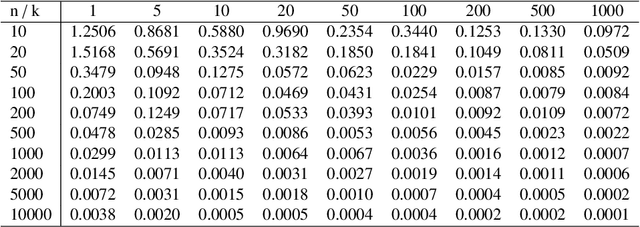
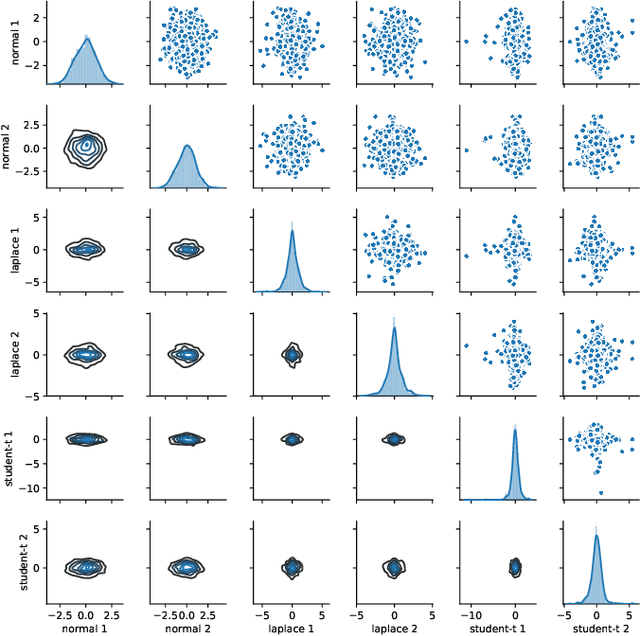
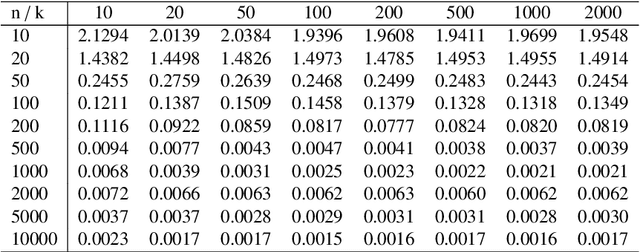
In this work we introduce a novel paradigm for Bayesian learning based on optimal transport theory. Namely, we propose to use the Wasserstein barycenter of the posterior law on models, as an alternative to the maximum a posteriori estimator and Bayesian model average. We exhibit conditions granting the existence and consistency of this estimator, discuss some of its basic and specific properties, and provide insight for practical implementations relying on standard sampling in finite-dimensional parameter spaces. We thus contribute to the recent blooming of applications of optimal transport theory in machine learning, beyond the discrete setting so far considered. The advantages of the proposed estimator are presented in theoretical terms and through analytical and numeral examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge