Gloria Feher
Accelerating Spherical k-Means
Jul 08, 2021


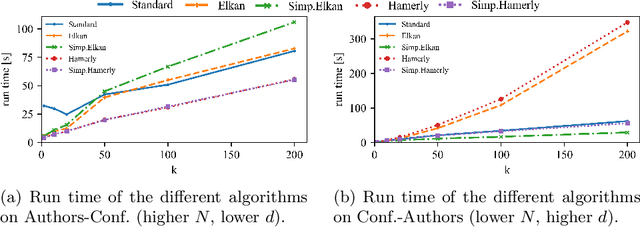
Abstract:Spherical k-means is a widely used clustering algorithm for sparse and high-dimensional data such as document vectors. While several improvements and accelerations have been introduced for the original k-means algorithm, not all easily translate to the spherical variant: Many acceleration techniques, such as the algorithms of Elkan and Hamerly, rely on the triangle inequality of Euclidean distances. However, spherical k-means uses Cosine similarities instead of distances for computational efficiency. In this paper, we incorporate the Elkan and Hamerly accelerations to the spherical k-means algorithm working directly with the Cosines instead of Euclidean distances to obtain a substantial speedup and evaluate these spherical accelerations on real data.
Retrieving Multi-Entity Associations: An Evaluation of Combination Modes for Word Embeddings
May 22, 2019



Abstract:Word embeddings have gained significant attention as learnable representations of semantic relations between words, and have been shown to improve upon the results of traditional word representations. However, little effort has been devoted to using embeddings for the retrieval of entity associations beyond pairwise relations. In this paper, we use popular embedding methods to train vector representations of an entity-annotated news corpus, and evaluate their performance for the task of predicting entity participation in news events versus a traditional word cooccurrence network as a baseline. To support queries for events with multiple participating entities, we test a number of combination modes for the embedding vectors. While we find that even the best combination modes for word embeddings do not quite reach the performance of the full cooccurrence network, especially for rare entities, we observe that different embedding methods model different types of relations, thereby indicating the potential for ensemble methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge