Accelerating k-Means Clustering with Cover Trees

The k-means clustering algorithm is a popular algorithm that partitions data into k clusters. There are many improvements to accelerate the standard algorithm. Most current research employs upper and lower bounds on point-to-cluster distances and the triangle inequality to reduce the number of distance computations, with only arrays as underlying data structures. These approaches cannot exploit that nearby points are likely assigned to the same cluster. We propose a new k-means algorithm based on the cover tree index, that has relatively low overhead and performs well, for a wider parameter range, than previous approaches based on the k-d tree. By combining this with upper and lower bounds, as in state-of-the-art approaches, we obtain a hybrid algorithm that combines the benefits of tree aggregation and bounds-based filtering.

Explicit Formulae to Interchangeably use Hyperplanes and Hyperballs using Inversive Geometry

Many algorithms require discriminative boundaries, such as separating hyperplanes or hyperballs, or are specifically designed to work on spherical data. By applying inversive geometry, we show that the two discriminative boundaries can be used interchangeably, and that general Euclidean data can be transformed into spherical data, whenever a change in point distances is acceptable. We provide explicit formulae to embed general Euclidean data into spherical data and to unembed it back. We further show a duality between hyperspherical caps, i.e., the volume created by a separating hyperplane on spherical data, and hyperballs and provide explicit formulae to map between the two. We further provide equations to translate inner products and Euclidean distances between the two spaces, to avoid explicit embedding and unembedding. We also provide a method to enforce projections of the general Euclidean space onto hemi-hyperspheres and propose an intrinsic dimensionality based method to obtain "all-purpose" parameters. To show the usefulness of the cap-ball-duality, we discuss example applications in machine learning and vector similarity search.

Medoid Silhouette clustering with automatic cluster number selection

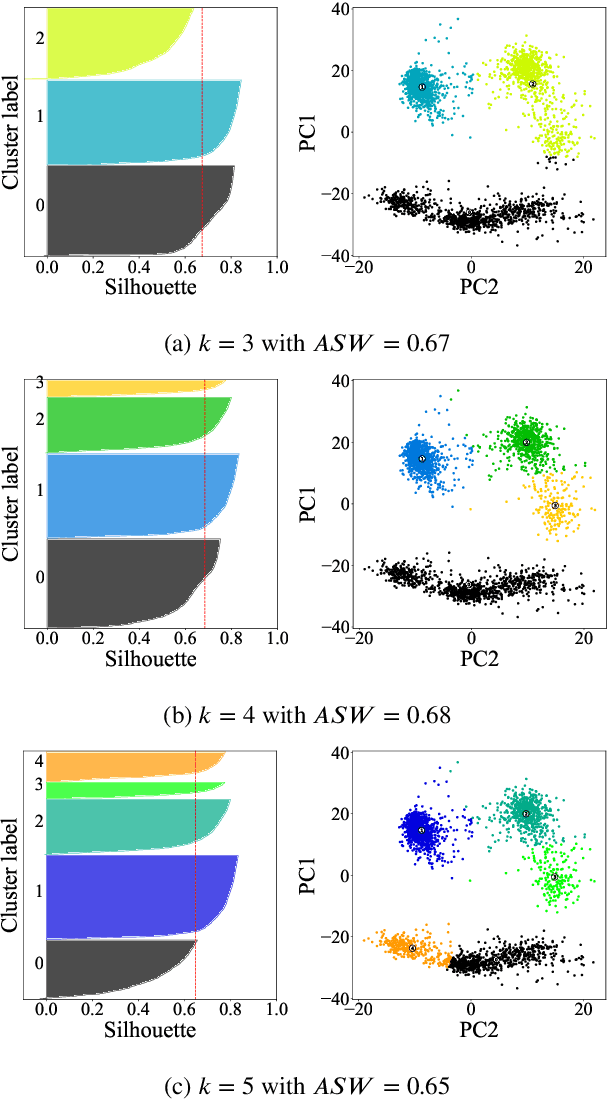
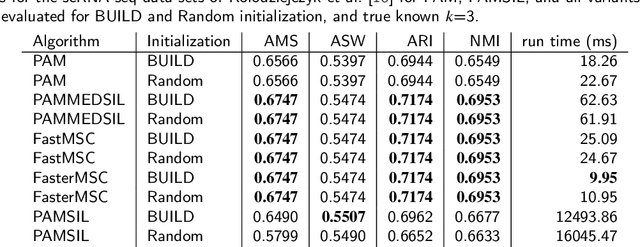
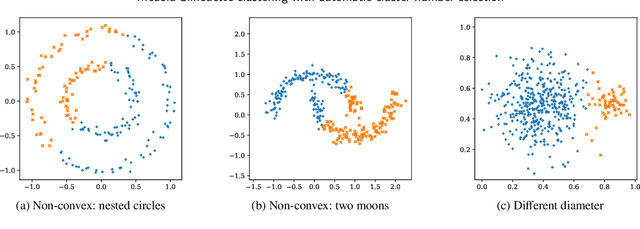
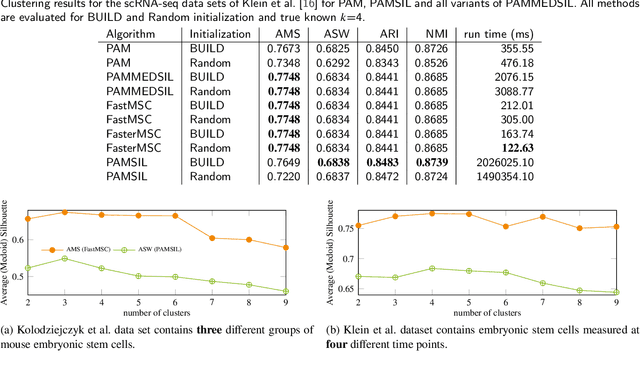
The evaluation of clustering results is difficult, highly dependent on the evaluated data set and the perspective of the beholder. There are many different clustering quality measures, which try to provide a general measure to validate clustering results. A very popular measure is the Silhouette. We discuss the efficient medoid-based variant of the Silhouette, perform a theoretical analysis of its properties, provide two fast versions for the direct optimization, and discuss the use to choose the optimal number of clusters. We combine ideas from the original Silhouette with the well-known PAM algorithm and its latest improvements FasterPAM. One of the versions guarantees equal results to the original variant and provides a run speedup of $O(k^2)$. In experiments on real data with 30000 samples and $k$=100, we observed a 10464$\times$ speedup compared to the original PAMMEDSIL algorithm. Additionally, we provide a variant to choose the optimal number of clusters directly.

Data Aggregation for Hierarchical Clustering

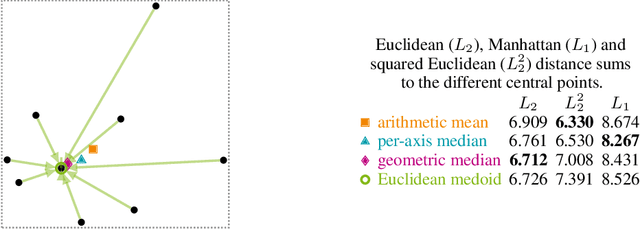
Hierarchical Agglomerative Clustering (HAC) is likely the earliest and most flexible clustering method, because it can be used with many distances, similarities, and various linkage strategies. It is often used when the number of clusters the data set forms is unknown and some sort of hierarchy in the data is plausible. Most algorithms for HAC operate on a full distance matrix, and therefore require quadratic memory. The standard algorithm also has cubic runtime to produce a full hierarchy. Both memory and runtime are especially problematic in the context of embedded or otherwise very resource-constrained systems. In this section, we present how data aggregation with BETULA, a numerically stable version of the well known BIRCH data aggregation algorithm, can be used to make HAC viable on systems with constrained resources with only small losses on clustering quality, and hence allow exploratory data analysis of very large data sets.

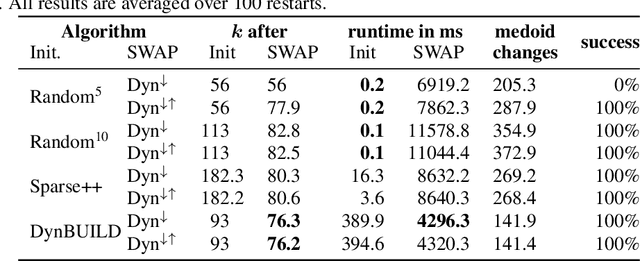
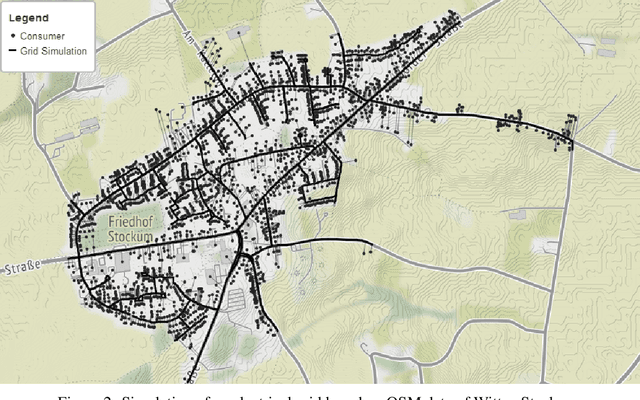
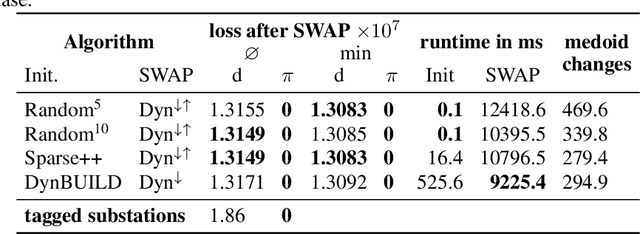
Sparse Partitioning Around Medoids

Partitioning Around Medoids (PAM, k-Medoids) is a popular clustering technique to use with arbitrary distance functions or similarities, where each cluster is represented by its most central object, called the medoid or the discrete median. In operations research, this family of problems is also known as facility location problem (FLP). FastPAM recently introduced a speedup for large k to make it applicable for larger problems, but the method still has a runtime quadratic in N. In this chapter, we discuss a sparse and asymmetric variant of this problem, to be used for example on graph data such as road networks. By exploiting sparsity, we can avoid the quadratic runtime and memory requirements, and make this method scalable to even larger problems, as long as we are able to build a small enough graph of sufficient connectivity to perform local optimization. Furthermore, we consider asymmetric cases, where the set of medoids is not identical to the set of points to be covered (or in the interpretation of facility location, where the possible facility locations are not identical to the consumer locations). Because of sparsity, it may be impossible to cover all points with just k medoids for too small k, which would render the problem unsolvable, and this breaks common heuristics for finding a good starting condition. We, hence, consider determining k as a part of the optimization problem and propose to first construct a greedy initial solution with a larger k, then to optimize the problem by alternating between PAM-style "swap" operations where the result is improved by replacing medoids with better alternatives and "remove" operations to reduce the number of k until neither allows further improving the result quality. We demonstrate the usefulness of this method on a problem from electrical engineering, with the input graph derived from cartographic data.

LOSDD: Leave-Out Support Vector Data Description for Outlier Detection

Support Vector Machines have been successfully used for one-class classification (OCSVM, SVDD) when trained on clean data, but they work much worse on dirty data: outliers present in the training data tend to become support vectors, and are hence considered "normal". In this article, we improve the effectiveness to detect outliers in dirty training data with a leave-out strategy: by temporarily omitting one candidate at a time, this point can be judged using the remaining data only. We show that this is more effective at scoring the outlierness of points than using the slack term of existing SVM-based approaches. Identified outliers can then be removed from the data, such that outliers hidden by other outliers can be identified, to reduce the problem of masking. Naively, this approach would require training N individual SVMs (and training $O(N^2)$ SVMs when iteratively removing the worst outliers one at a time), which is prohibitively expensive. We will discuss that only support vectors need to be considered in each step and that by reusing SVM parameters and weights, this incremental retraining can be accelerated substantially. By removing candidates in batches, we can further improve the processing time, although it obviously remains more costly than training a single SVM.

Stop using the elbow criterion for k-means and how to choose the number of clusters instead

A major challenge when using k-means clustering often is how to choose the parameter k, the number of clusters. In this letter, we want to point out that it is very easy to draw poor conclusions from a common heuristic, the "elbow method". Better alternatives have been known in literature for a long time, and we want to draw attention to some of these easy to use options, that often perform better. This letter is a call to stop using the elbow method altogether, because it severely lacks theoretic support, and we want to encourage educators to discuss the problems of the method -- if introducing it in class at all -- and teach alternatives instead, while researchers and reviewers should reject conclusions drawn from the elbow method.

Clustering by Direct Optimization of the Medoid Silhouette

The evaluation of clustering results is difficult, highly dependent on the evaluated data set and the perspective of the beholder. There are many different clustering quality measures, which try to provide a general measure to validate clustering results. A very popular measure is the Silhouette. We discuss the efficient medoid-based variant of the Silhouette, perform a theoretical analysis of its properties, and provide two fast versions for the direct optimization. We combine ideas from the original Silhouette with the well-known PAM algorithm and its latest improvements FasterPAM. One of the versions guarantees equal results to the original variant and provides a run speedup of $O(k^2)$. In experiments on real data with 30000 samples and $k$=100, we observed a 10464$\times$ speedup compared to the original PAMMEDSIL algorithm.

On Projections to Linear Subspaces

The merit of projecting data onto linear subspaces is well known from, e.g., dimension reduction. One key aspect of subspace projections, the maximum preservation of variance (principal component analysis), has been thoroughly researched and the effect of random linear projections on measures such as intrinsic dimensionality still is an ongoing effort. In this paper, we investigate the less explored depths of linear projections onto explicit subspaces of varying dimensionality and the expectations of variance that ensue. The result is a new family of bounds for Euclidean distances and inner products. We showcase the quality of these bounds as well as investigate the intimate relation to intrinsic dimensionality estimation.

MESS: Manifold Embedding Motivated Super Sampling

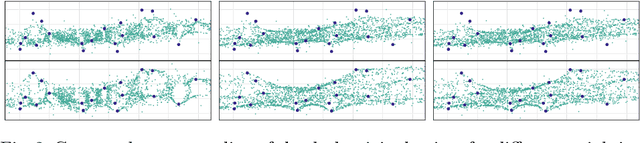
Many approaches in the field of machine learning and data analysis rely on the assumption that the observed data lies on lower-dimensional manifolds. This assumption has been verified empirically for many real data sets. To make use of this manifold assumption one generally requires the manifold to be locally sampled to a certain density such that features of the manifold can be observed. However, for increasing intrinsic dimensionality of a data set the required data density introduces the need for very large data sets, resulting in one of the many faces of the curse of dimensionality. To combat the increased requirement for local data density we propose a framework to generate virtual data points that faithful to an approximate embedding function underlying the manifold observable in the data.