Explicit Formulae to Interchangeably use Hyperplanes and Hyperballs using Inversive Geometry

Many algorithms require discriminative boundaries, such as separating hyperplanes or hyperballs, or are specifically designed to work on spherical data. By applying inversive geometry, we show that the two discriminative boundaries can be used interchangeably, and that general Euclidean data can be transformed into spherical data, whenever a change in point distances is acceptable. We provide explicit formulae to embed general Euclidean data into spherical data and to unembed it back. We further show a duality between hyperspherical caps, i.e., the volume created by a separating hyperplane on spherical data, and hyperballs and provide explicit formulae to map between the two. We further provide equations to translate inner products and Euclidean distances between the two spaces, to avoid explicit embedding and unembedding. We also provide a method to enforce projections of the general Euclidean space onto hemi-hyperspheres and propose an intrinsic dimensionality based method to obtain "all-purpose" parameters. To show the usefulness of the cap-ball-duality, we discuss example applications in machine learning and vector similarity search.

On Projections to Linear Subspaces

The merit of projecting data onto linear subspaces is well known from, e.g., dimension reduction. One key aspect of subspace projections, the maximum preservation of variance (principal component analysis), has been thoroughly researched and the effect of random linear projections on measures such as intrinsic dimensionality still is an ongoing effort. In this paper, we investigate the less explored depths of linear projections onto explicit subspaces of varying dimensionality and the expectations of variance that ensue. The result is a new family of bounds for Euclidean distances and inner products. We showcase the quality of these bounds as well as investigate the intimate relation to intrinsic dimensionality estimation.

MESS: Manifold Embedding Motivated Super Sampling

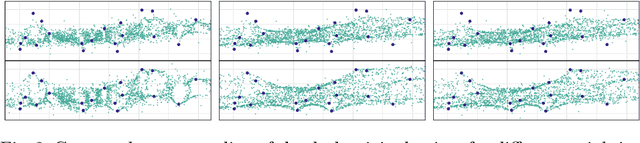
Many approaches in the field of machine learning and data analysis rely on the assumption that the observed data lies on lower-dimensional manifolds. This assumption has been verified empirically for many real data sets. To make use of this manifold assumption one generally requires the manifold to be locally sampled to a certain density such that features of the manifold can be observed. However, for increasing intrinsic dimensionality of a data set the required data density introduces the need for very large data sets, resulting in one of the many faces of the curse of dimensionality. To combat the increased requirement for local data density we propose a framework to generate virtual data points that faithful to an approximate embedding function underlying the manifold observable in the data.

ABID: Angle Based Intrinsic Dimensionality

The intrinsic dimensionality refers to the ``true'' dimensionality of the data, as opposed to the dimensionality of the data representation. For example, when attributes are highly correlated, the intrinsic dimensionality can be much lower than the number of variables. Local intrinsic dimensionality refers to the observation that this property can vary for different parts of the data set; and intrinsic dimensionality can serve as a proxy for the local difficulty of the data set. Most popular methods for estimating the local intrinsic dimensionality are based on distances, and the rate at which the distances to the nearest neighbors increase, a concept known as ``expansion dimension''. In this paper we introduce an orthogonal concept, which does not use any distances: we use the distribution of angles between neighbor points. We derive the theoretical distribution of angles and use this to construct an estimator for intrinsic dimensionality. Experimentally, we verify that this measure behaves similarly, but complementarily, to existing measures of intrinsic dimensionality. By introducing a new idea of intrinsic dimensionality to the research community, we hope to contribute to a better understanding of intrinsic dimensionality and to spur new research in this direction.