Accelerating k-Means Clustering with Cover Trees

The k-means clustering algorithm is a popular algorithm that partitions data into k clusters. There are many improvements to accelerate the standard algorithm. Most current research employs upper and lower bounds on point-to-cluster distances and the triangle inequality to reduce the number of distance computations, with only arrays as underlying data structures. These approaches cannot exploit that nearby points are likely assigned to the same cluster. We propose a new k-means algorithm based on the cover tree index, that has relatively low overhead and performs well, for a wider parameter range, than previous approaches based on the k-d tree. By combining this with upper and lower bounds, as in state-of-the-art approaches, we obtain a hybrid algorithm that combines the benefits of tree aggregation and bounds-based filtering.

Data Aggregation for Hierarchical Clustering

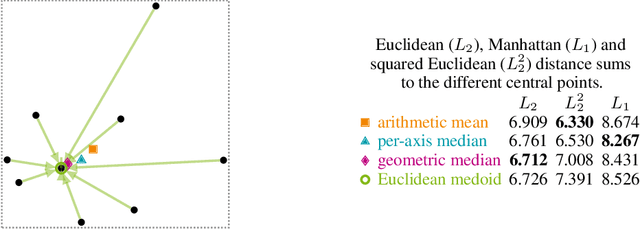
Hierarchical Agglomerative Clustering (HAC) is likely the earliest and most flexible clustering method, because it can be used with many distances, similarities, and various linkage strategies. It is often used when the number of clusters the data set forms is unknown and some sort of hierarchy in the data is plausible. Most algorithms for HAC operate on a full distance matrix, and therefore require quadratic memory. The standard algorithm also has cubic runtime to produce a full hierarchy. Both memory and runtime are especially problematic in the context of embedded or otherwise very resource-constrained systems. In this section, we present how data aggregation with BETULA, a numerically stable version of the well known BIRCH data aggregation algorithm, can be used to make HAC viable on systems with constrained resources with only small losses on clustering quality, and hence allow exploratory data analysis of very large data sets.

Accelerating Spherical k-Means

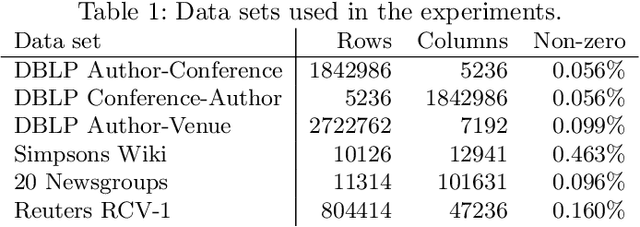
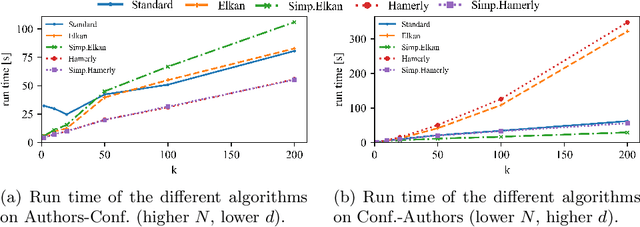
Spherical k-means is a widely used clustering algorithm for sparse and high-dimensional data such as document vectors. While several improvements and accelerations have been introduced for the original k-means algorithm, not all easily translate to the spherical variant: Many acceleration techniques, such as the algorithms of Elkan and Hamerly, rely on the triangle inequality of Euclidean distances. However, spherical k-means uses Cosine similarities instead of distances for computational efficiency. In this paper, we incorporate the Elkan and Hamerly accelerations to the spherical k-means algorithm working directly with the Cosines instead of Euclidean distances to obtain a substantial speedup and evaluate these spherical accelerations on real data.

BETULA: Numerically Stable CF-Trees for BIRCH Clustering

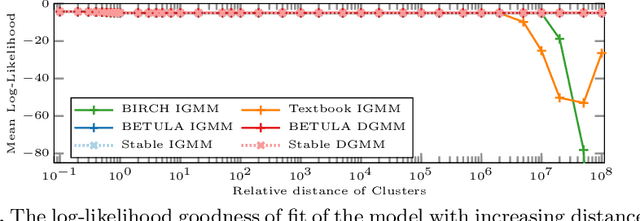
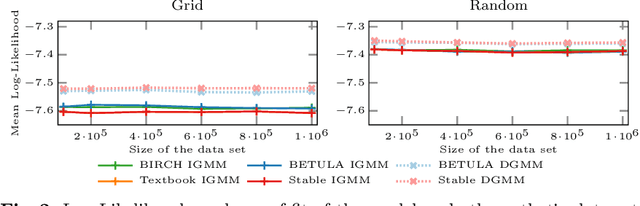
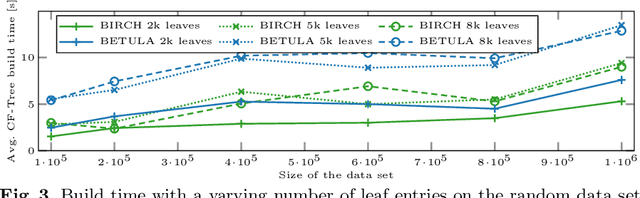
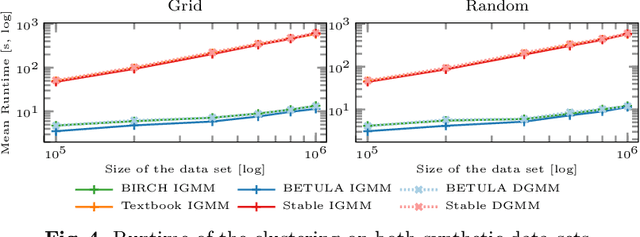
BIRCH clustering is a widely known approach for clustering, that has influenced much subsequent research and commercial products. The key contribution of BIRCH is the Clustering Feature tree (CF-Tree), which is a compressed representation of the input data. As new data arrives, the tree is eventually rebuilt to increase the compression. Afterward, the leaves of the tree are used for clustering. Because of the data compression, this method is very scalable. The idea has been adopted for example for k-means, data stream, and density-based clustering. Clustering features used by BIRCH are simple summary statistics that can easily be updated with new data: the number of points, the linear sums, and the sum of squared values. Unfortunately, how the sum of squares is then used in BIRCH is prone to catastrophic cancellation. We introduce a replacement cluster feature that does not have this numeric problem, that is not much more expensive to maintain, and which makes many computations simpler and hence more efficient. These cluster features can also easily be used in other work derived from BIRCH, such as algorithms for streaming data. In the experiments, we demonstrate the numerical problem and compare the performance of the original algorithm compared to the improved cluster features.