Robust Transfer Learning for Active Level Set Estimation with Locally Adaptive Gaussian Process Prior

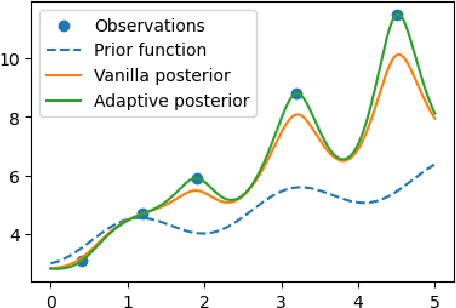
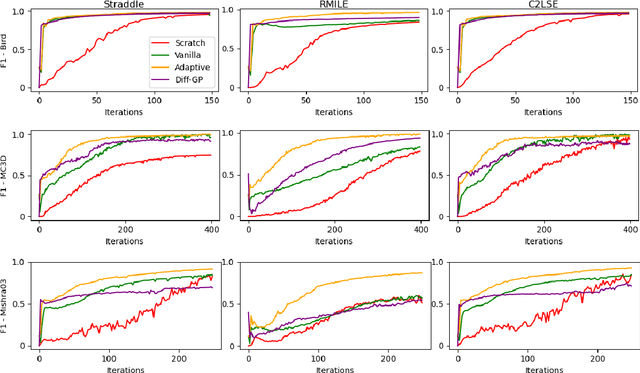
The objective of active level set estimation for a black-box function is to precisely identify regions where the function values exceed or fall below a specified threshold by iteratively performing function evaluations to gather more information about the function. This becomes particularly important when function evaluations are costly, drastically limiting our ability to acquire large datasets. A promising way to sample-efficiently model the black-box function is by incorporating prior knowledge from a related function. However, this approach risks slowing down the estimation task if the prior knowledge is irrelevant or misleading. In this paper, we present a novel transfer learning method for active level set estimation that safely integrates a given prior knowledge while constantly adjusting it to guarantee a robust performance of a level set estimation algorithm even when the prior knowledge is irrelevant. We theoretically analyze this algorithm to show that it has a better level set convergence compared to standard transfer learning approaches that do not make any adjustment to the prior. Additionally, extensive experiments across multiple datasets confirm the effectiveness of our method when applied to various different level set estimation algorithms as well as different transfer learning scenarios.

Active Level Set Estimation for Continuous Search Space with Theoretical Guarantee

A common problem encountered in many real-world applications is level set estimation where the goal is to determine the region in the function domain where the function is above or below a given threshold. When the function is black-box and expensive to evaluate, the level sets need to be found in a minimum set of function evaluations. Existing methods often assume a discrete search space with a finite set of data points for function evaluations and estimating the level sets. When applied to a continuous search space, these methods often need to first discretize the space which leads to poor results while needing high computational time. While some methods cater for the continuous setting, they still lack a proper guarantee for theoretical convergence. To address this problem, we propose a novel algorithm that does not need any discretization and can directly work in continuous search spaces. Our method suggests points by constructing an acquisition function that is defined as a measure of confidence of the function being higher or lower than the given threshold. A theoretical analysis for the convergence of the algorithm to an accurate solution is provided. On multiple synthetic and real-world datasets, our algorithm successfully outperforms state-of-the-art methods.

Evolutionary bagged ensemble learning

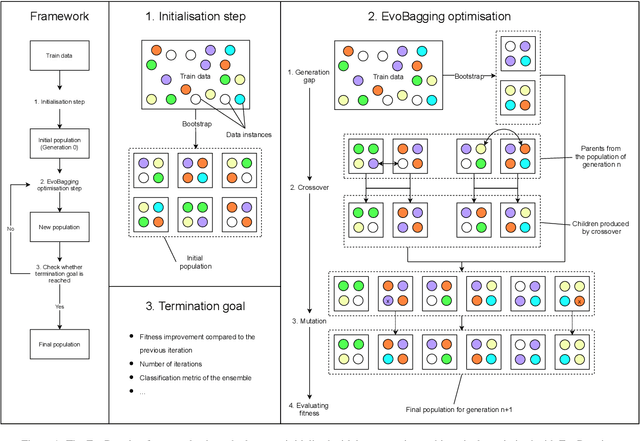
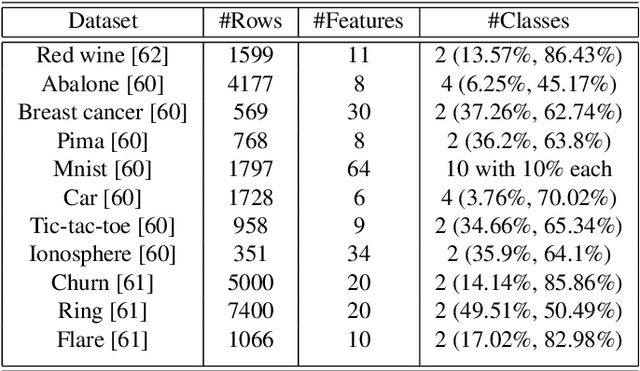
Ensemble learning has gained success in machine learning with major advantages over other learning methods. Bagging is a prominent ensemble learning method that creates subgroups of data, known as bags, that are trained by individual machine learning methods such as decision trees. Random forest is a prominent example of bagging with additional features in the learning process. \textcolor{black}{A limitation of bagging is high bias (model under-fitting) in the aggregated prediction when the individual learners have high biases.} Evolutionary algorithms have been prominent for optimisation problems and also been used for machine learning. Evolutionary algorithms are gradient-free methods with a population of candidate solutions that maintain diversity for creating new solutions. In conventional bagged ensemble learning, the bags are created once and the content, in terms of the training examples, is fixed over the learning process. In our paper, we propose evolutionary bagged ensemble learning, where we utilise evolutionary algorithms to evolve the content of the bags in order to enhance the ensemble by providing diversity in the bags iteratively. The results show that our evolutionary ensemble bagging method outperforms conventional ensemble methods (bagging and random forests) for several benchmark datasets under certain constraints. Evolutionary bagging can inherently sustain a diverse set of bags without sacrificing any data.