Learning Hash Function through Codewords

In this paper, we propose a novel hash learning approach that has the following main distinguishing features, when compared to past frameworks. First, the codewords are utilized in the Hamming space as ancillary techniques to accomplish its hash learning task. These codewords, which are inferred from the data, attempt to capture grouping aspects of the data's hash codes. Furthermore, the proposed framework is capable of addressing supervised, unsupervised and, even, semi-supervised hash learning scenarios. Additionally, the framework adopts a regularization term over the codewords, which automatically chooses the codewords for the problem. To efficiently solve the problem, one Block Coordinate Descent algorithm is showcased in the paper. We also show that one step of the algorithms can be casted into several Support Vector Machine problems which enables our algorithms to utilize efficient software package. For the regularization term, a closed form solution of the proximal operator is provided in the paper. A series of comparative experiments focused on content-based image retrieval highlights its performance advantages.

Reduced-Rank Local Distance Metric Learning for k-NN Classification

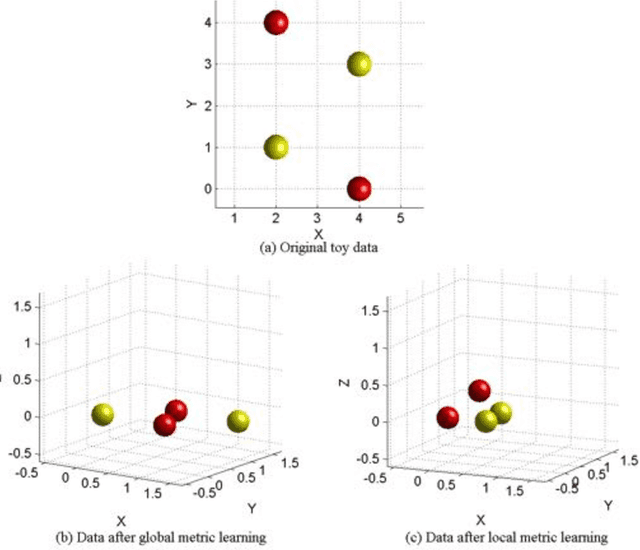
We propose a new method for local distance metric learning based on sample similarity as side information. These local metrics, which utilize conical combinations of metric weight matrices, are learned from the pooled spatial characteristics of the data, as well as the similarity profiles between the pairs of samples, whose distances are measured. The main objective of our framework is to yield metrics, such that the resulting distances between similar samples are small and distances between dissimilar samples are above a certain threshold. For learning and inference purposes, we describe a transductive, as well as an inductive algorithm; the former approach naturally befits our framework, while the latter one is provided in the interest of faster learning. Experimental results on a collection of classification problems imply that the new methods may exhibit notable performance advantages over alternative metric learning approaches that have recently appeared in the literature.

Hash Function Learning via Codewords

In this paper we introduce a novel hash learning framework that has two main distinguishing features, when compared to past approaches. First, it utilizes codewords in the Hamming space as ancillary means to accomplish its hash learning task. These codewords, which are inferred from the data, attempt to capture similarity aspects of the data's hash codes. Secondly and more importantly, the same framework is capable of addressing supervised, unsupervised and, even, semi-supervised hash learning tasks in a natural manner. A series of comparative experiments focused on content-based image retrieval highlights its performance advantages.

Multi-Task Learning with Group-Specific Feature Space Sharing

When faced with learning a set of inter-related tasks from a limited amount of usable data, learning each task independently may lead to poor generalization performance. Multi-Task Learning (MTL) exploits the latent relations between tasks and overcomes data scarcity limitations by co-learning all these tasks simultaneously to offer improved performance. We propose a novel Multi-Task Multiple Kernel Learning framework based on Support Vector Machines for binary classification tasks. By considering pair-wise task affinity in terms of similarity between a pair's respective feature spaces, the new framework, compared to other similar MTL approaches, offers a high degree of flexibility in determining how similar feature spaces should be, as well as which pairs of tasks should share a common feature space in order to benefit overall performance. The associated optimization problem is solved via a block coordinate descent, which employs a consensus-form Alternating Direction Method of Multipliers algorithm to optimize the Multiple Kernel Learning weights and, hence, to determine task affinities. Empirical evaluation on seven data sets exhibits a statistically significant improvement of our framework's results compared to the ones of several other Clustered Multi-Task Learning methods.

Conic Multi-Task Classification

Traditionally, Multi-task Learning (MTL) models optimize the average of task-related objective functions, which is an intuitive approach and which we will be referring to as Average MTL. However, a more general framework, referred to as Conic MTL, can be formulated by considering conic combinations of the objective functions instead; in this framework, Average MTL arises as a special case, when all combination coefficients equal 1. Although the advantage of Conic MTL over Average MTL has been shown experimentally in previous works, no theoretical justification has been provided to date. In this paper, we derive a generalization bound for the Conic MTL method, and demonstrate that the tightest bound is not necessarily achieved, when all combination coefficients equal 1; hence, Average MTL may not always be the optimal choice, and it is important to consider Conic MTL. As a byproduct of the generalization bound, it also theoretically explains the good experimental results of previous relevant works. Finally, we propose a new Conic MTL model, whose conic combination coefficients minimize the generalization bound, instead of choosing them heuristically as has been done in previous methods. The rationale and advantage of our model is demonstrated and verified via a series of experiments by comparing with several other methods.

Kernel-based Distance Metric Learning in the Output Space

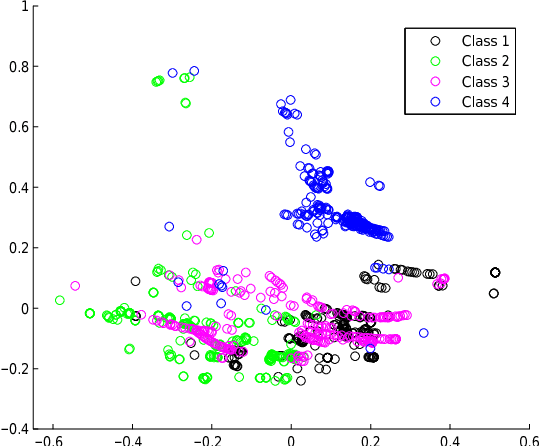
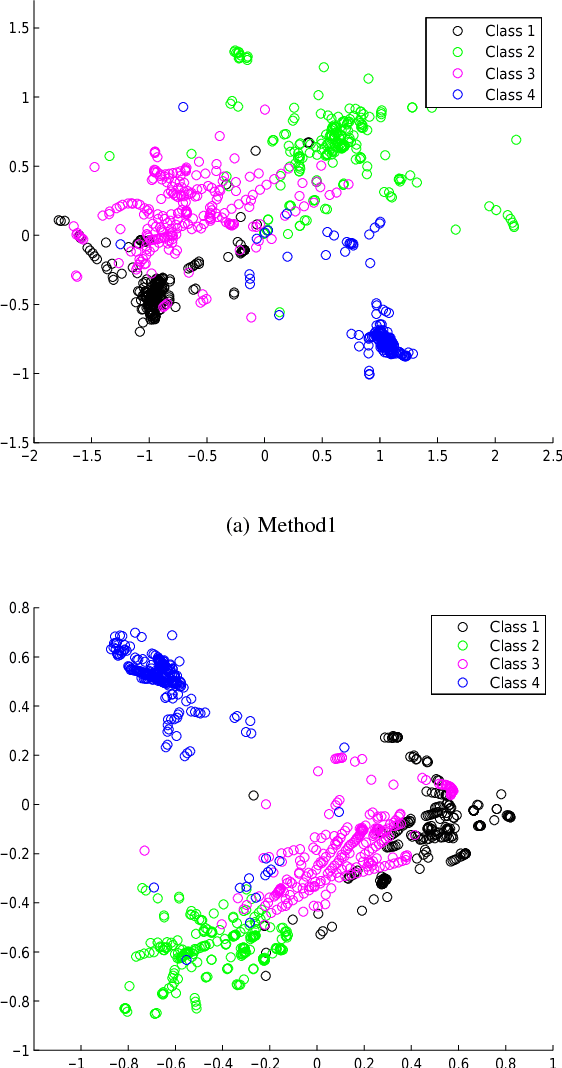
In this paper we present two related, kernel-based Distance Metric Learning (DML) methods. Their respective models non-linearly map data from their original space to an output space, and subsequent distance measurements are performed in the output space via a Mahalanobis metric. The dimensionality of the output space can be directly controlled to facilitate the learning of a low-rank metric. Both methods allow for simultaneous inference of the associated metric and the mapping to the output space, which can be used to visualize the data, when the output space is 2- or 3-dimensional. Experimental results for a collection of classification tasks illustrate the advantages of the proposed methods over other traditional and kernel-based DML approaches.

Pareto-Path Multi-Task Multiple Kernel Learning

A traditional and intuitively appealing Multi-Task Multiple Kernel Learning (MT-MKL) method is to optimize the sum (thus, the average) of objective functions with (partially) shared kernel function, which allows information sharing amongst tasks. We point out that the obtained solution corresponds to a single point on the Pareto Front (PF) of a Multi-Objective Optimization (MOO) problem, which considers the concurrent optimization of all task objectives involved in the Multi-Task Learning (MTL) problem. Motivated by this last observation and arguing that the former approach is heuristic, we propose a novel Support Vector Machine (SVM) MT-MKL framework, that considers an implicitly-defined set of conic combinations of task objectives. We show that solving our framework produces solutions along a path on the aforementioned PF and that it subsumes the optimization of the average of objective functions as a special case. Using algorithms we derived, we demonstrate through a series of experimental results that the framework is capable of achieving better classification performance, when compared to other similar MTL approaches.

A Unifying Framework for Typical Multi-Task Multiple Kernel Learning Problems

Over the past few years, Multi-Kernel Learning (MKL) has received significant attention among data-driven feature selection techniques in the context of kernel-based learning. MKL formulations have been devised and solved for a broad spectrum of machine learning problems, including Multi-Task Learning (MTL). Solving different MKL formulations usually involves designing algorithms that are tailored to the problem at hand, which is, typically, a non-trivial accomplishment. In this paper we present a general Multi-Task Multi-Kernel Learning (Multi-Task MKL) framework that subsumes well-known Multi-Task MKL formulations, as well as several important MKL approaches on single-task problems. We then derive a simple algorithm that can solve the unifying framework. To demonstrate the flexibility of the proposed framework, we formulate a new learning problem, namely Partially-Shared Common Space (PSCS) Multi-Task MKL, and demonstrate its merits through experimentation.

Multi-Task Classification Hypothesis Space with Improved Generalization Bounds

This paper presents a RKHS, in general, of vector-valued functions intended to be used as hypothesis space for multi-task classification. It extends similar hypothesis spaces that have previously considered in the literature. Assuming this space, an improved Empirical Rademacher Complexity-based generalization bound is derived. The analysis is itself extended to an MKL setting. The connection between the proposed hypothesis space and a Group-Lasso type regularizer is discussed. Finally, experimental results, with some SVM-based Multi-Task Learning problems, underline the quality of the derived bounds and validate the paper's analysis.