Kernel-based Distance Metric Learning in the Output Space
Paper and Code
Apr 28, 2014

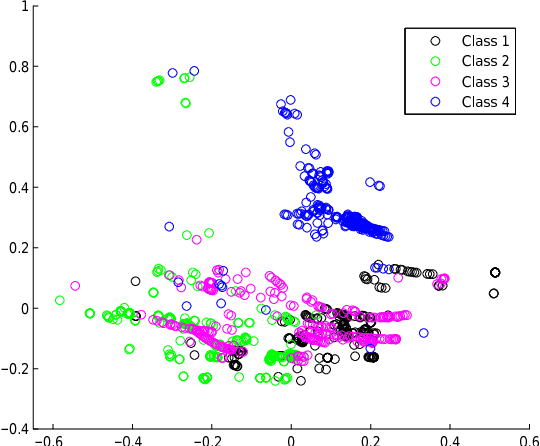
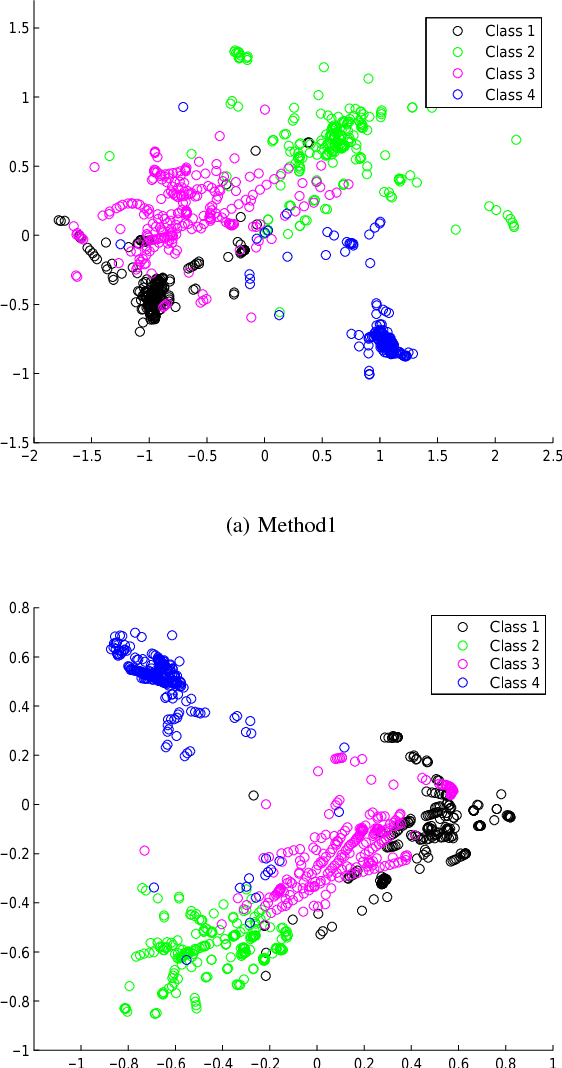
In this paper we present two related, kernel-based Distance Metric Learning (DML) methods. Their respective models non-linearly map data from their original space to an output space, and subsequent distance measurements are performed in the output space via a Mahalanobis metric. The dimensionality of the output space can be directly controlled to facilitate the learning of a low-rank metric. Both methods allow for simultaneous inference of the associated metric and the mapping to the output space, which can be used to visualize the data, when the output space is 2- or 3-dimensional. Experimental results for a collection of classification tasks illustrate the advantages of the proposed methods over other traditional and kernel-based DML approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge