Reduced-Rank Local Distance Metric Learning for k-NN Classification
Paper and Code
Feb 21, 2019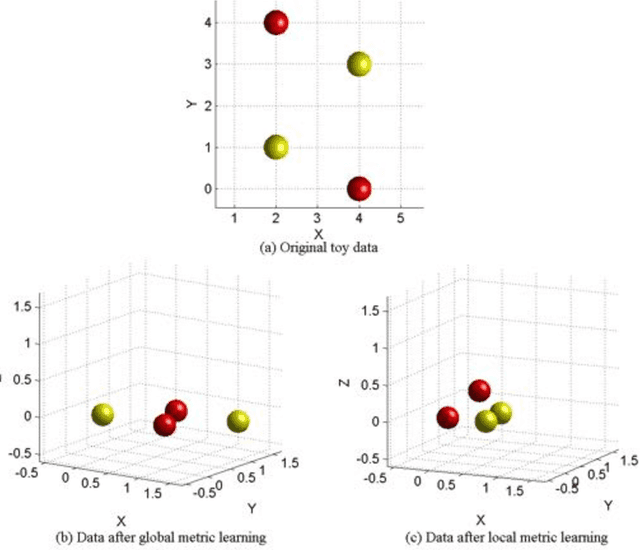



We propose a new method for local distance metric learning based on sample similarity as side information. These local metrics, which utilize conical combinations of metric weight matrices, are learned from the pooled spatial characteristics of the data, as well as the similarity profiles between the pairs of samples, whose distances are measured. The main objective of our framework is to yield metrics, such that the resulting distances between similar samples are small and distances between dissimilar samples are above a certain threshold. For learning and inference purposes, we describe a transductive, as well as an inductive algorithm; the former approach naturally befits our framework, while the latter one is provided in the interest of faster learning. Experimental results on a collection of classification problems imply that the new methods may exhibit notable performance advantages over alternative metric learning approaches that have recently appeared in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge