Learning to rank quantum circuits for hardware-optimized performance enhancement

We introduce and experimentally test a machine-learning-based method for ranking logically equivalent quantum circuits based on expected performance estimates derived from a training procedure conducted on real hardware. We apply our method to the problem of layout selection, in which abstracted qubits are assigned to physical qubits on a given device. Circuit measurements performed on IBM hardware indicate that the maximum and median fidelities of logically equivalent layouts can differ by an order of magnitude. We introduce a circuit score used for ranking that is parameterized in terms of a physics-based, phenomenological error model whose parameters are fit by training a ranking-loss function over a measured dataset. The dataset consists of quantum circuits exhibiting a diversity of structures and executed on IBM hardware, allowing the model to incorporate the contextual nature of real device noise and errors without the need to perform an exponentially costly tomographic protocol. We perform model training and execution on the 16-qubit ibmq_guadalupe device and compare our method to two common approaches: random layout selection and a publicly available baseline called Mapomatic. Our model consistently outperforms both approaches, predicting layouts that exhibit lower noise and higher performance. In particular, we find that our best model leads to a $1.8\times$ reduction in selection error when compared to the baseline approach and a $3.2\times$ reduction when compared to random selection. Beyond delivering a new form of predictive quantum characterization, verification, and validation, our results reveal the specific way in which context-dependent and coherent gate errors appear to dominate the divergence from performance estimates extrapolated from simple proxy measures.

A Rubik's Cube inspired approach to Clifford synthesis

The problem of decomposing an arbitrary Clifford element into a sequence of Clifford gates is known as Clifford synthesis. Drawing inspiration from similarities between this and the famous Rubik's Cube problem, we develop a machine learning approach for Clifford synthesis based on learning an approximation to the distance to the identity. This approach is probabilistic and computationally intensive. However, when a decomposition is successfully found, it often involves fewer gates than existing synthesis algorithms. Additionally, our approach is much more flexible than existing algorithms in that arbitrary gate sets, device topologies, and gate fidelities may incorporated, thus allowing for the approach to be tailored to a specific device.

Empirical Evaluation of Physical Adversarial Patch Attacks Against Overhead Object Detection Models

Adversarial patches are images designed to fool otherwise well-performing neural network-based computer vision models. Although these attacks were initially conceived of and studied digitally, in that the raw pixel values of the image were perturbed, recent work has demonstrated that these attacks can successfully transfer to the physical world. This can be accomplished by printing out the patch and adding it into scenes of newly captured images or video footage. In this work we further test the efficacy of adversarial patch attacks in the physical world under more challenging conditions. We consider object detection models trained on overhead imagery acquired through aerial or satellite cameras, and we test physical adversarial patches inserted into scenes of a desert environment. Our main finding is that it is far more difficult to successfully implement the adversarial patch attacks under these conditions than in the previously considered conditions. This has important implications for AI safety as the real-world threat posed by adversarial examples may be overstated.

Deep Generative Modeling in Network Science with Applications to Public Policy Research

Network data is increasingly being used in quantitative, data-driven public policy research. These are typically very rich datasets that contain complex correlations and inter-dependencies. This richness both promises to be quite useful for policy research, while at the same time posing a challenge for the useful extraction of information from these datasets - a challenge which calls for new data analysis methods. In this report, we formulate a research agenda of key methodological problems whose solutions would enable new advances across many areas of policy research. We then review recent advances in applying deep learning to network data, and show how these methods may be used to address many of the methodological problems we identified. We particularly emphasize deep generative methods, which can be used to generate realistic synthetic networks useful for microsimulation and agent-based models capable of informing key public policy questions. We extend these recent advances by developing a new generative framework which applies to large social contact networks commonly used in epidemiological modeling. For context, we also compare and contrast these recent neural network-based approaches with the more traditional Exponential Random Graph Models. Lastly, we discuss some open problems where more progress is needed.

A Probability Density Theory for Spin-Glass Systems

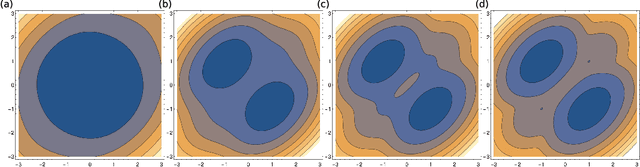
Spin-glass systems are universal models for representing many-body phenomena in statistical physics and computer science. High quality solutions of NP-hard combinatorial optimization problems can be encoded into low energy states of spin-glass systems. In general, evaluating the relevant physical and computational properties of such models is difficult due to critical slowing down near a phase transition. Ideally, one could use recent advances in deep learning for characterizing the low-energy properties of these complex systems. Unfortunately, many of the most promising machine learning approaches are only valid for distributions over continuous variables and thus cannot be directly applied to discrete spin-glass models. To this end, we develop a continuous probability density theory for spin-glass systems with arbitrary dimensions, interactions, and local fields. We show how our formulation geometrically encodes key physical and computational properties of the spin-glass in an instance-wise fashion without the need for quenched disorder averaging. We show that our approach is beyond the mean-field theory and identify a transition from a convex to non-convex energy landscape as the temperature is lowered past a critical temperature. We apply our formalism to a number of spin-glass models including the Sherrington-Kirkpatrick (SK) model, spins on random Erd\H{o}s-R\'enyi graphs, and random restricted Boltzmann machines.

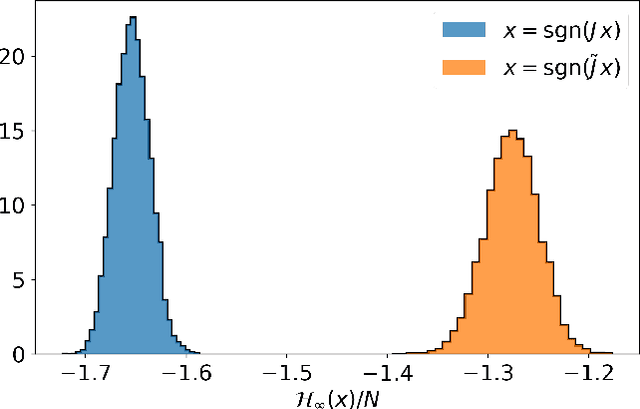
Self-Supervised Learning of Generative Spin-Glasses with Normalizing Flows

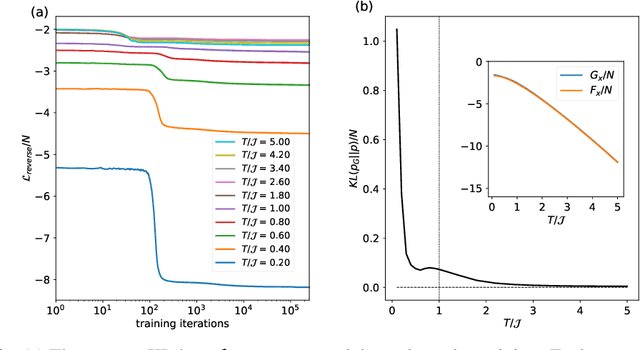
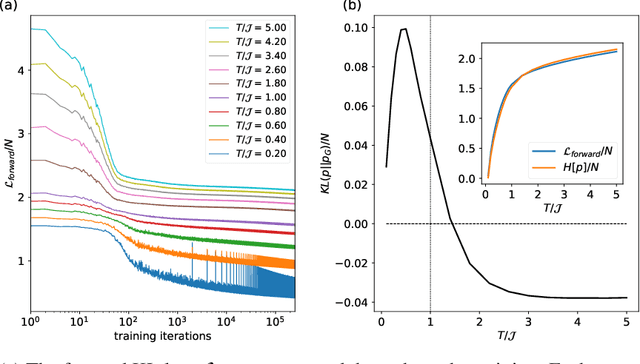
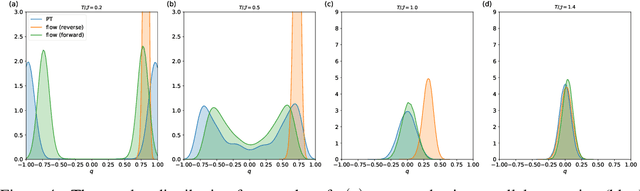
Spin-glasses are universal models that can capture complex behavior of many-body systems at the interface of statistical physics and computer science including discrete optimization, inference in graphical models, and automated reasoning. Computing the underlying structure and dynamics of such complex systems is extremely difficult due to the combinatorial explosion of their state space. Here, we develop deep generative continuous spin-glass distributions with normalizing flows to model correlations in generic discrete problems. We use a self-supervised learning paradigm by automatically generating the data from the spin-glass itself. We demonstrate that key physical and computational properties of the spin-glass phase can be successfully learned, including multi-modal steady-state distributions and topological structures among metastable states. Remarkably, we observe that the learning itself corresponds to a spin-glass phase transition within the layers of the trained normalizing flows. The inverse normalizing flows learns to perform reversible multi-scale coarse-graining operations which are very different from the typical irreversible renormalization group techniques.

Adversarial Examples for Cost-Sensitive Classifiers

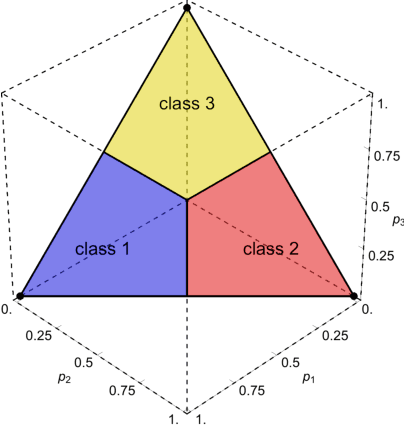
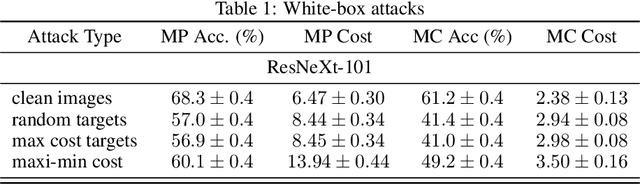
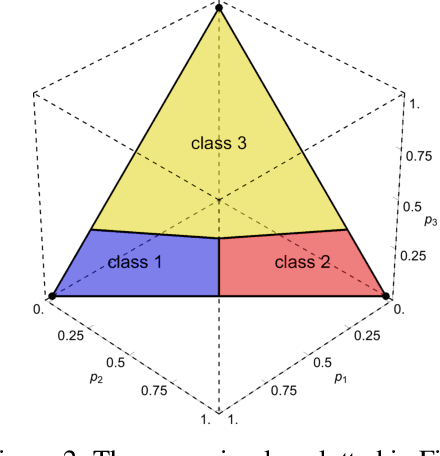
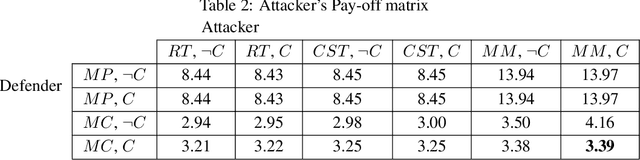
Motivated by safety-critical classification problems, we investigate adversarial attacks against cost-sensitive classifiers. We use current state-of-the-art adversarially-resistant neural network classifiers [1] as the underlying models. Cost-sensitive predictions are then achieved via a final processing step in the feed-forward evaluation of the network. We evaluate the effectiveness of cost-sensitive classifiers against a variety of attacks and we introduce a new cost-sensitive attack which performs better than targeted attacks in some cases. We also explored the measures a defender can take in order to limit their vulnerability to these attacks. This attacker/defender scenario is naturally framed as a two-player zero-sum finite game which we analyze using game theory.