Self-Supervised Learning of Generative Spin-Glasses with Normalizing Flows

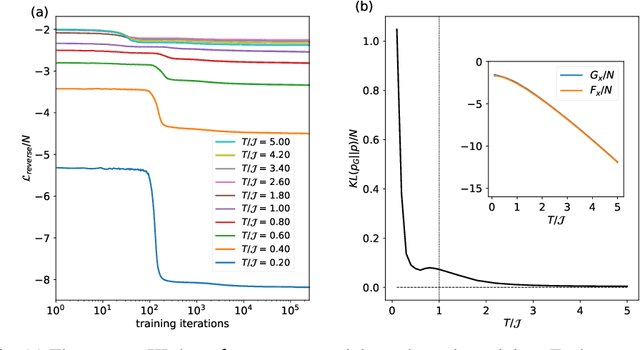
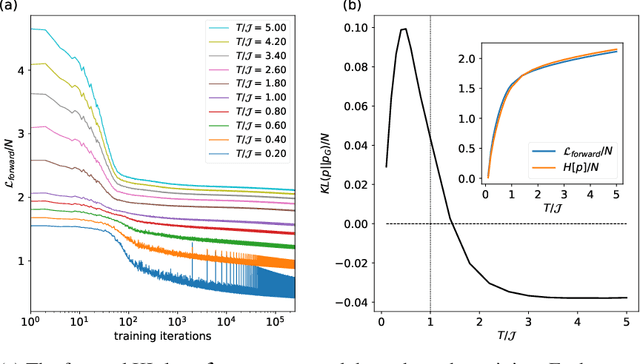
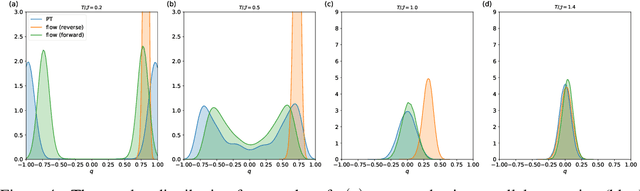
Spin-glasses are universal models that can capture complex behavior of many-body systems at the interface of statistical physics and computer science including discrete optimization, inference in graphical models, and automated reasoning. Computing the underlying structure and dynamics of such complex systems is extremely difficult due to the combinatorial explosion of their state space. Here, we develop deep generative continuous spin-glass distributions with normalizing flows to model correlations in generic discrete problems. We use a self-supervised learning paradigm by automatically generating the data from the spin-glass itself. We demonstrate that key physical and computational properties of the spin-glass phase can be successfully learned, including multi-modal steady-state distributions and topological structures among metastable states. Remarkably, we observe that the learning itself corresponds to a spin-glass phase transition within the layers of the trained normalizing flows. The inverse normalizing flows learns to perform reversible multi-scale coarse-graining operations which are very different from the typical irreversible renormalization group techniques.