Semi-Supervised Machine Learning: a Homological Approach

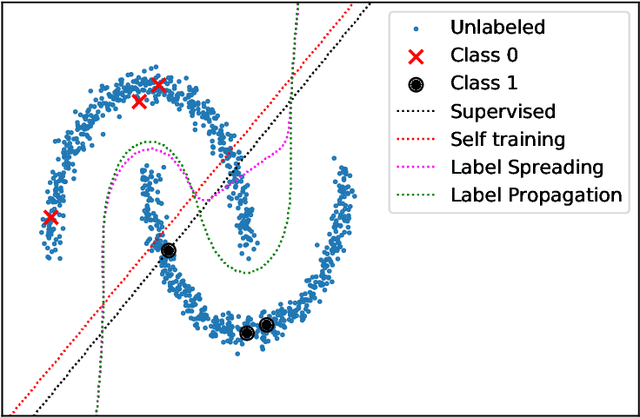
In this paper we describe the mathematical foundations of a new approach to semi-supervised Machine Learning. Using techniques of Symbolic Computation and Computer Algebra, we apply the concept of persistent homology to obtain a new semi-supervised learning method.

A Topological Approach for Semi-Supervised Learning

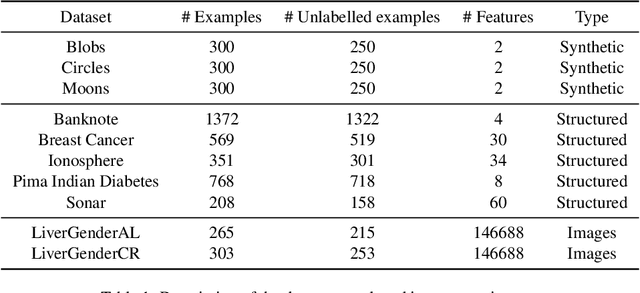
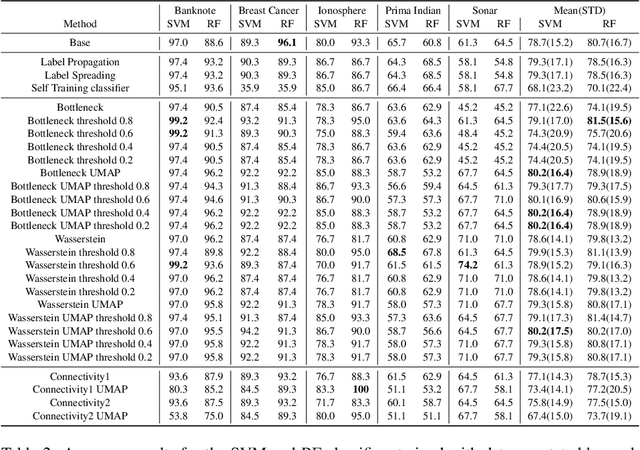
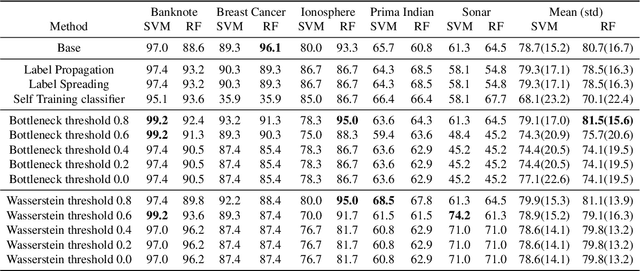
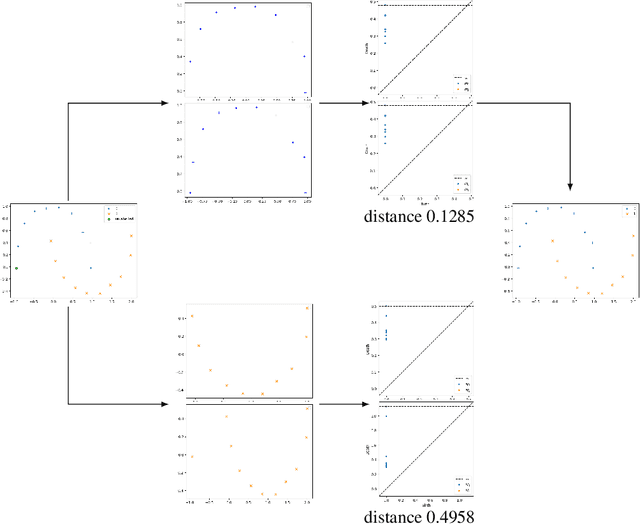
Nowadays, Machine Learning and Deep Learning methods have become the state-of-the-art approach to solve data classification tasks. In order to use those methods, it is necessary to acquire and label a considerable amount of data; however, this is not straightforward in some fields, since data annotation is time consuming and might require expert knowledge. This challenge can be tackled by means of semi-supervised learning methods that take advantage of both labelled and unlabelled data. In this work, we present new semi-supervised learning methods based on techniques from Topological Data Analysis (TDA), a field that is gaining importance for analysing large amounts of data with high variety and dimensionality. In particular, we have created two semi-supervised learning methods following two different topological approaches. In the former, we have used a homological approach that consists in studying the persistence diagrams associated with the data using the Bottleneck and Wasserstein distances. In the latter, we have taken into account the connectivity of the data. In addition, we have carried out a thorough analysis of the developed methods using 3 synthetic datasets, 5 structured datasets, and 2 datasets of images. The results show that the semi-supervised methods developed in this work outperform both the results obtained with models trained with only manually labelled data, and those obtained with classical semi-supervised learning methods, reaching improvements of up to a 16%.

Neuron detection in stack images: a persistent homology interpretation

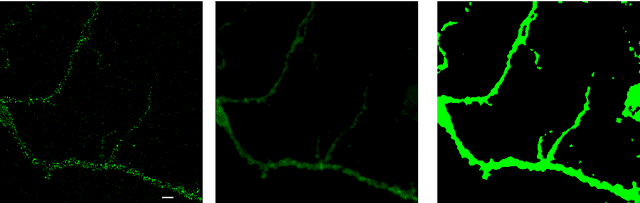
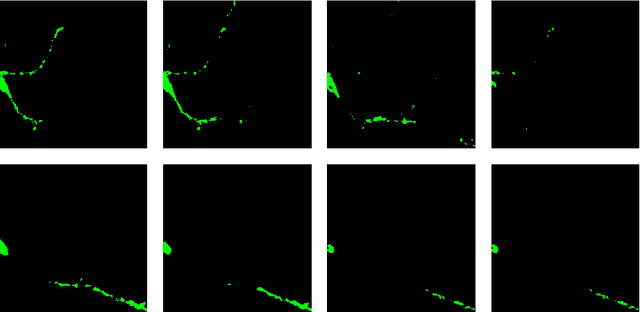
Automation and reliability are the two main requirements when computers are applied in Life Sciences. In this paper we report on an application to neuron recognition, an important step in our long-term project of providing software systems to the study of neural morphology and functionality from biomedical images. Our algorithms have been implemented in an ImageJ plugin called NeuronPersistentJ, which has been validated experimentally. The soundness and reliability of our approach are based on the interpretation of our processing methods with respect to persistent homology, a well-known tool in computational mathematics.

SynapCountJ --- a Tool for Analyzing Synaptic Densities in Neurons

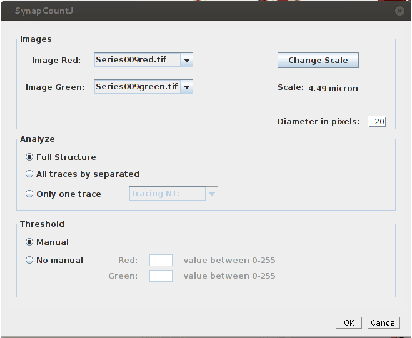
The quantification of synapses is instrumental to measure the evolution of synaptic densities of neurons under the effect of some physiological conditions, neuronal diseases or even drug treatments. However, the manual quantification of synapses is a tedious, error-prone, time-consuming and subjective task; therefore, tools that might automate this process are desirable. In this paper, we present SynapCountJ, an ImageJ plugin, that can measure synaptic density of individual neurons obtained by immunofluorescence techniques, and also can be applied for batch processing of neurons that have been obtained in the same experiment or using the same setting. The procedure to quantify synapses implemented in SynapCountJ is based on the colocalization of three images of the same neuron (the neuron marked with two antibody markers and the structure of the neuron) and is inspired by methods coming from Computational Algebraic Topology. SynapCountJ provides a procedure to semi-automatically quantify the number of synapses of neuron cultures; as a result, the time required for such an analysis is greatly reduced.

Verifying a platform for digital imaging: a multi-tool strategy

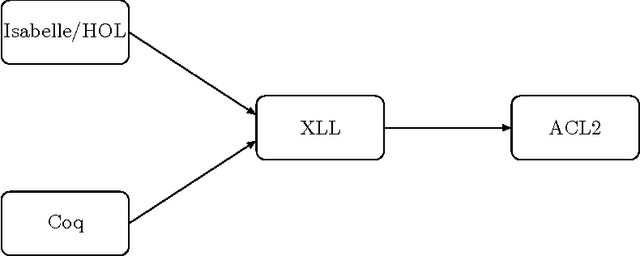
Fiji is a Java platform widely used by biologists and other experimental scientists to process digital images. In particular, in our research - made together with a biologists team; we use Fiji in some pre-processing steps before undertaking a homological digital processing of images. In a previous work, we have formalised the correctness of the programs which use homological techniques to analyse digital images. However, the verification of Fiji's pre-processing step was missed. In this paper, we present a multi-tool approach filling this gap, based on the combination of Why/Krakatoa, Coq and ACL2.