SynapCountJ --- a Tool for Analyzing Synaptic Densities in Neurons

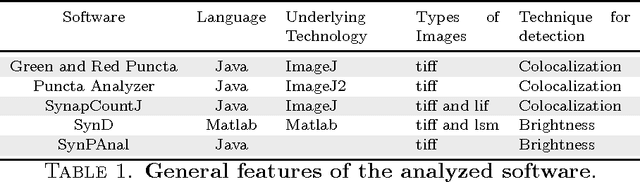
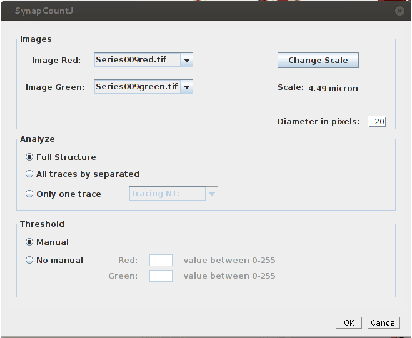
The quantification of synapses is instrumental to measure the evolution of synaptic densities of neurons under the effect of some physiological conditions, neuronal diseases or even drug treatments. However, the manual quantification of synapses is a tedious, error-prone, time-consuming and subjective task; therefore, tools that might automate this process are desirable. In this paper, we present SynapCountJ, an ImageJ plugin, that can measure synaptic density of individual neurons obtained by immunofluorescence techniques, and also can be applied for batch processing of neurons that have been obtained in the same experiment or using the same setting. The procedure to quantify synapses implemented in SynapCountJ is based on the colocalization of three images of the same neuron (the neuron marked with two antibody markers and the structure of the neuron) and is inspired by methods coming from Computational Algebraic Topology. SynapCountJ provides a procedure to semi-automatically quantify the number of synapses of neuron cultures; as a result, the time required for such an analysis is greatly reduced.

Effective persistent homology of digital images

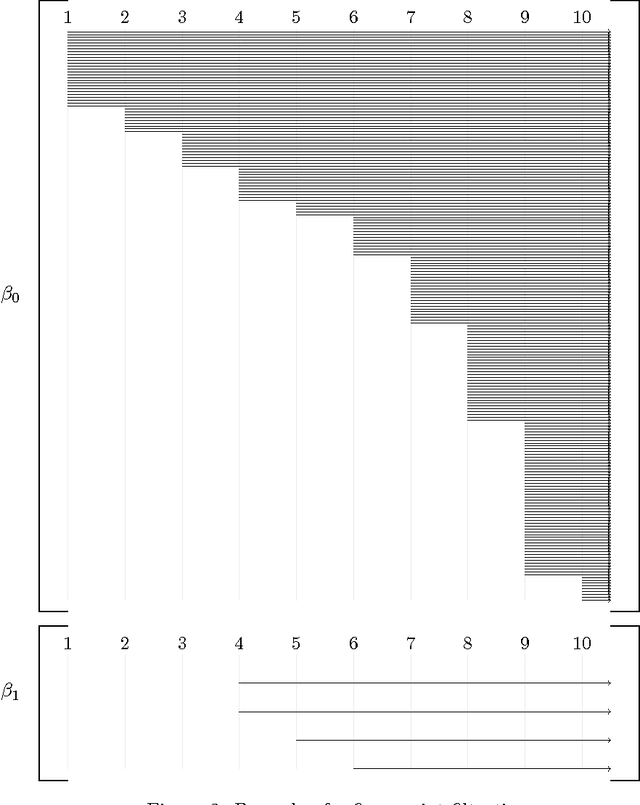
In this paper, three Computational Topology methods (namely effective homology, persistent homology and discrete vector fields) are mixed together to produce algorithms for homological digital image processing. The algorithms have been implemented as extensions of the Kenzo system and have shown a good performance when applied on some actual images extracted from a public dataset.

Verifying a platform for digital imaging: a multi-tool strategy

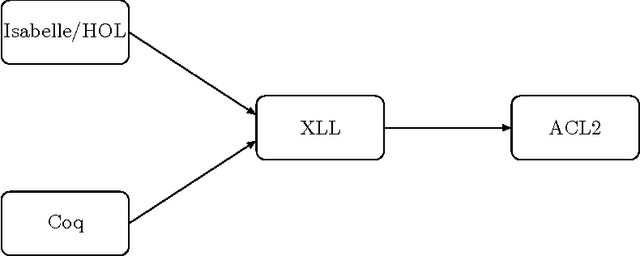
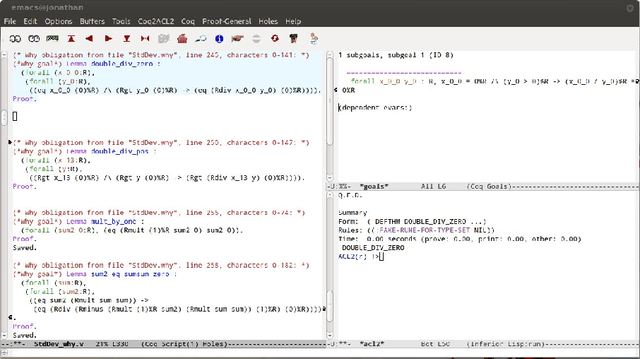
Fiji is a Java platform widely used by biologists and other experimental scientists to process digital images. In particular, in our research - made together with a biologists team; we use Fiji in some pre-processing steps before undertaking a homological digital processing of images. In a previous work, we have formalised the correctness of the programs which use homological techniques to analyse digital images. However, the verification of Fiji's pre-processing step was missed. In this paper, we present a multi-tool approach filling this gap, based on the combination of Why/Krakatoa, Coq and ACL2.

Integrating multiple sources to answer questions in Algebraic Topology

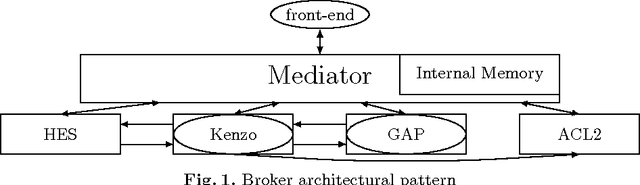
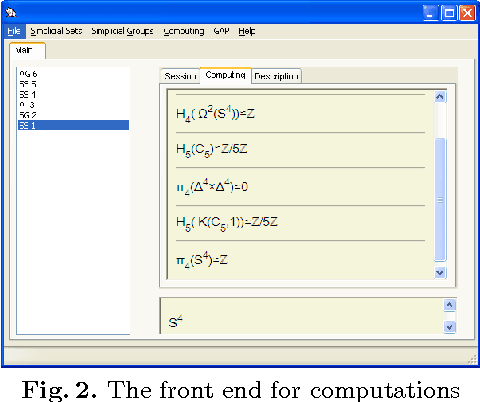
We present in this paper an evolution of a tool from a user interface for a concrete Computer Algebra system for Algebraic Topology (the Kenzo system), to a front-end allowing the interoperability among different sources for computation and deduction. The architecture allows the system not only to interface several systems, but also to make them cooperate in shared calculations.