Semi-Supervised Machine Learning: a Homological Approach

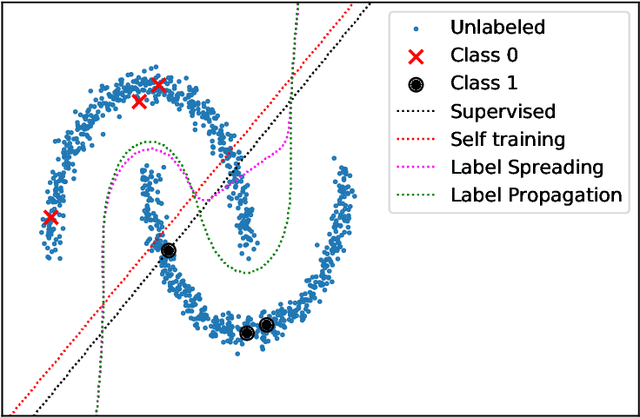
In this paper we describe the mathematical foundations of a new approach to semi-supervised Machine Learning. Using techniques of Symbolic Computation and Computer Algebra, we apply the concept of persistent homology to obtain a new semi-supervised learning method.

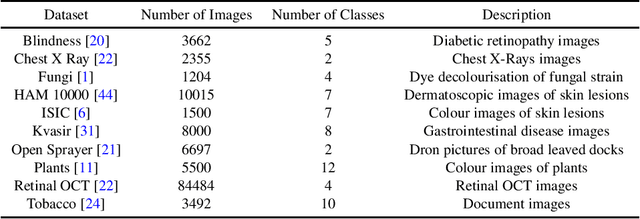
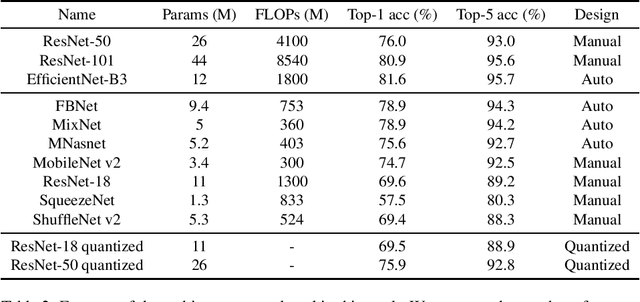
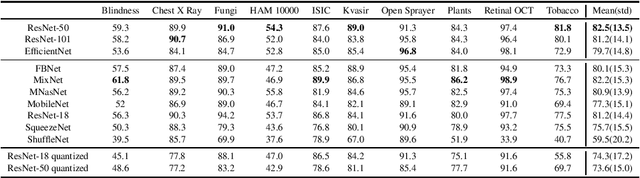
Semi-Supervised Learning for Image Classification using Compact Networks in the BioMedical Context

The development of mobile and on the edge applications that embed deep convolutional neural models has the potential to revolutionise biomedicine. However, most deep learning models require computational resources that are not available in smartphones or edge devices; an issue that can be faced by means of compact models. The problem with such models is that they are, at least usually, less accurate than bigger models. In this work, we study how this limitation can be addressed with the application of semi-supervised learning techniques. We conduct several statistical analyses to compare performance of deep compact architectures when trained using semi-supervised learning methods for tackling image classification tasks in the biomedical context. In particular, we explore three families of compact networks, and two families of semi-supervised learning techniques for 10 biomedical tasks. By combining semi-supervised learning methods with compact networks, it is possible to obtain a similar performance to standard size networks. In general, the best results are obtained when combining data distillation with MixNet, and plain distillation with ResNet-18. Also, in general, NAS networks obtain better results than manually designed networks and quantized networks. The work presented in this paper shows the benefits of apply semi-supervised methods to compact networks; this allow us to create compact models that are not only as accurate as standard size models, but also faster and lighter. Finally, we have developed a library that simplifies the construction of compact models using semi-supervised learning methods.

A Topological Approach for Semi-Supervised Learning

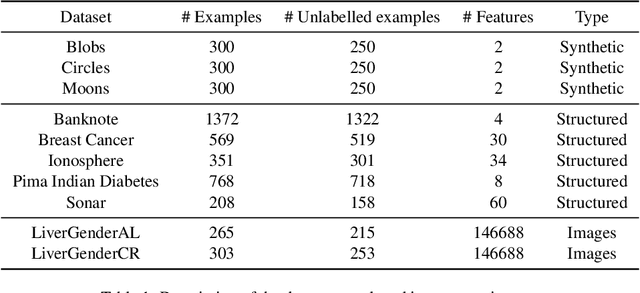
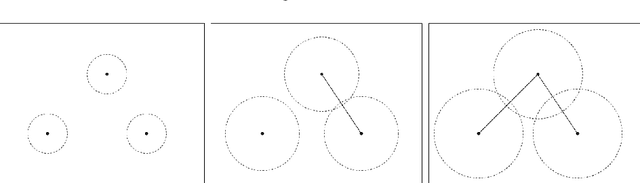
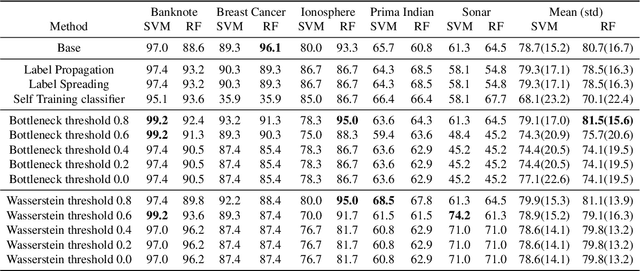
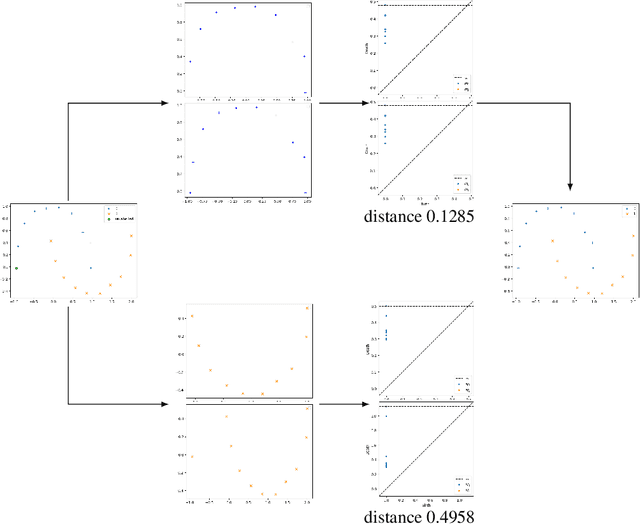
Nowadays, Machine Learning and Deep Learning methods have become the state-of-the-art approach to solve data classification tasks. In order to use those methods, it is necessary to acquire and label a considerable amount of data; however, this is not straightforward in some fields, since data annotation is time consuming and might require expert knowledge. This challenge can be tackled by means of semi-supervised learning methods that take advantage of both labelled and unlabelled data. In this work, we present new semi-supervised learning methods based on techniques from Topological Data Analysis (TDA), a field that is gaining importance for analysing large amounts of data with high variety and dimensionality. In particular, we have created two semi-supervised learning methods following two different topological approaches. In the former, we have used a homological approach that consists in studying the persistence diagrams associated with the data using the Bottleneck and Wasserstein distances. In the latter, we have taken into account the connectivity of the data. In addition, we have carried out a thorough analysis of the developed methods using 3 synthetic datasets, 5 structured datasets, and 2 datasets of images. The results show that the semi-supervised methods developed in this work outperform both the results obtained with models trained with only manually labelled data, and those obtained with classical semi-supervised learning methods, reaching improvements of up to a 16%.