Learning Consistent Causal Abstraction Networks

Causal artificial intelligence aims to enhance explainability, trustworthiness, and robustness in AI by leveraging structural causal models (SCMs). In this pursuit, recent advances formalize network sheaves and cosheaves of causal knowledge. Pushing in the same direction, we tackle the learning of consistent causal abstraction network (CAN), a sheaf-theoretic framework where (i) SCMs are Gaussian, (ii) restriction maps are transposes of constructive linear causal abstractions (CAs) adhering to the semantic embedding principle, and (iii) edge stalks correspond--up to permutation--to the node stalks of more detailed SCMs. Our problem formulation separates into edge-specific local Riemannian problems and avoids nonconvex objectives. We propose an efficient search procedure, solving the local problems with SPECTRAL, our iterative method with closed-form updates and suitable for positive definite and semidefinite covariance matrices. Experiments on synthetic data show competitive performance in the CA learning task, and successful recovery of diverse CAN structures.

The Relativity of Causal Knowledge

Recent advances in artificial intelligence reveal the limits of purely predictive systems and call for a shift toward causal and collaborative reasoning. Drawing inspiration from the revolution of Grothendieck in mathematics, we introduce the relativity of causal knowledge, which posits structural causal models (SCMs) are inherently imperfect, subjective representations embedded within networks of relationships. By leveraging category theory, we arrange SCMs into a functor category and show that their observational and interventional probability measures naturally form convex structures. This result allows us to encode non-intervened SCMs with convex spaces of probability measures. Next, using sheaf theory, we construct the network sheaf and cosheaf of causal knowledge. These structures enable the transfer of causal knowledge across the network while incorporating interventional consistency and the perspective of the subjects, ultimately leading to the formal, mathematical definition of relative causal knowledge.

Learning Multi-Frequency Partial Correlation Graphs

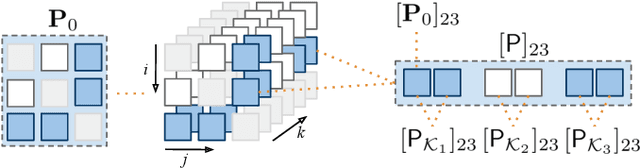
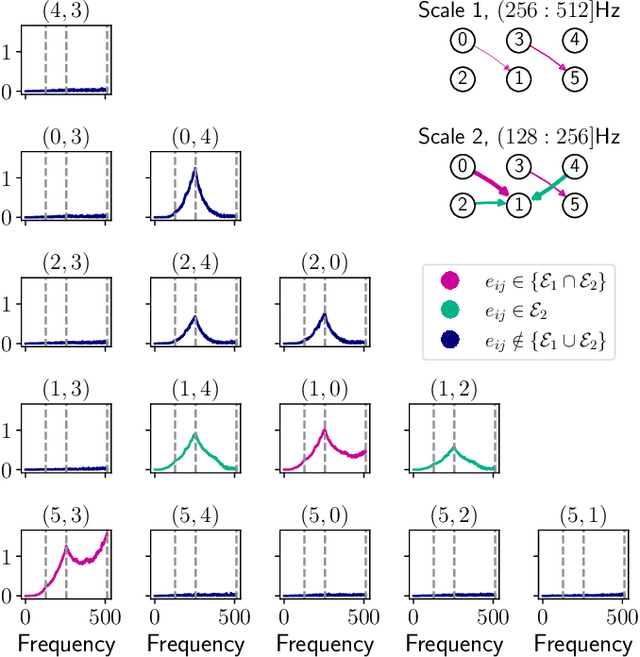
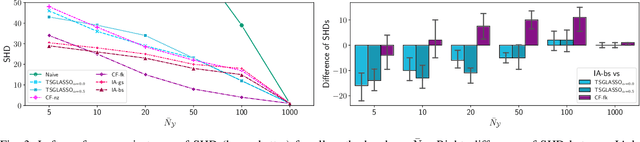
Despite the large research effort devoted to learning dependencies between time series, the state of the art still faces a major limitation: existing methods learn partial correlations but fail to discriminate across distinct frequency bands. Motivated by many applications in which this differentiation is pivotal, we overcome this limitation by learning a block-sparse, frequency-dependent, partial correlation graph, in which layers correspond to different frequency bands, and partial correlations can occur over just a few layers. To this aim, we formulate and solve two nonconvex learning problems: the first has a closed-form solution and is suitable when there is prior knowledge about the number of partial correlations; the second hinges on an iterative solution based on successive convex approximation, and is effective for the general case where no prior knowledge is available. Numerical results on synthetic data show that the proposed methods outperform the current state of the art. Finally, the analysis of financial time series confirms that partial correlations exist only within a few frequency bands, underscoring how our methods enable the gaining of valuable insights that would be undetected without discriminating along the frequency domain.

Extracting the Multiscale Causal Backbone of Brain Dynamics

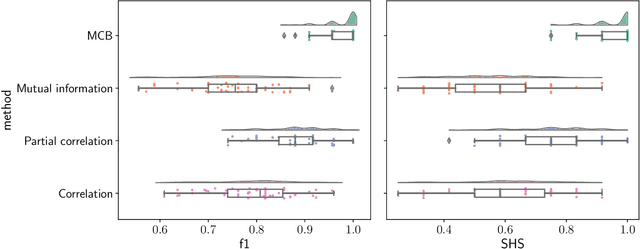
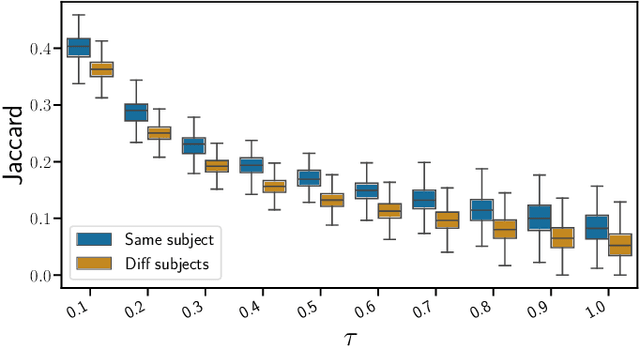
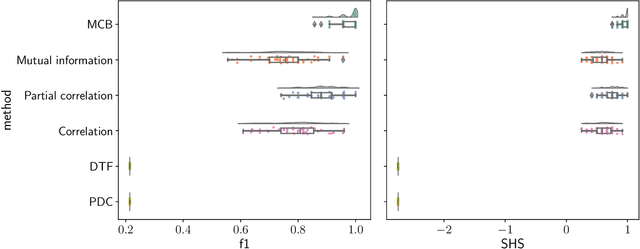
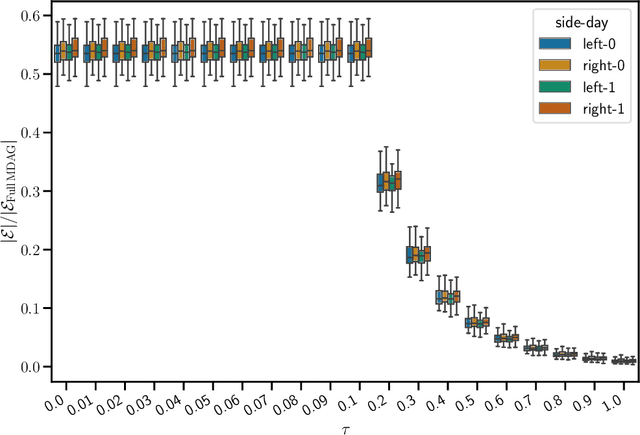
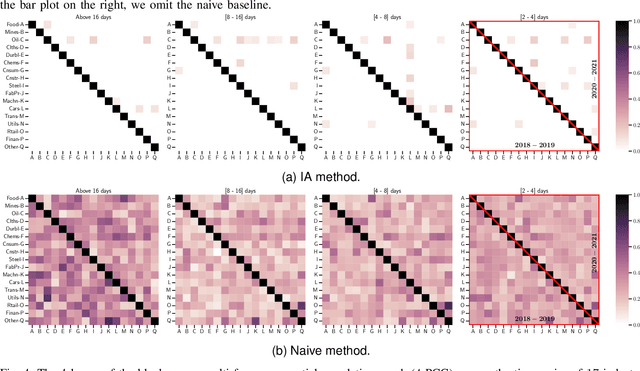
The bulk of the research effort on brain connectivity revolves around statistical associations among brain regions, which do not directly relate to the causal mechanisms governing brain dynamics. Here we propose the multiscale causal backbone (MCB) of brain dynamics shared by a set of individuals across multiple temporal scales, and devise a principled methodology to extract it. Our approach leverages recent advances in multiscale causal structure learning and optimizes the trade-off between the model fitting and its complexity. Empirical assessment on synthetic data shows the superiority of our methodology over a baseline based on canonical functional connectivity networks. When applied to resting-state fMRI data, we find sparse MCBs for both the left and right brain hemispheres. Thanks to its multiscale nature, our approach shows that at low-frequency bands, causal dynamics are driven by brain regions associated with high-level cognitive functions; at higher frequencies instead, nodes related to sensory processing play a crucial role. Finally, our analysis of individual multiscale causal structures confirms the existence of a causal fingerprint of brain connectivity, thus supporting from a causal perspective the existing extensive research in brain connectivity fingerprinting.

Multiscale Non-stationary Causal Structure Learning from Time Series Data

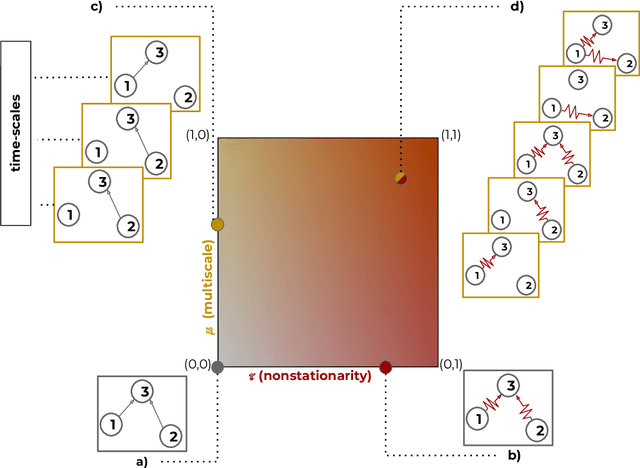
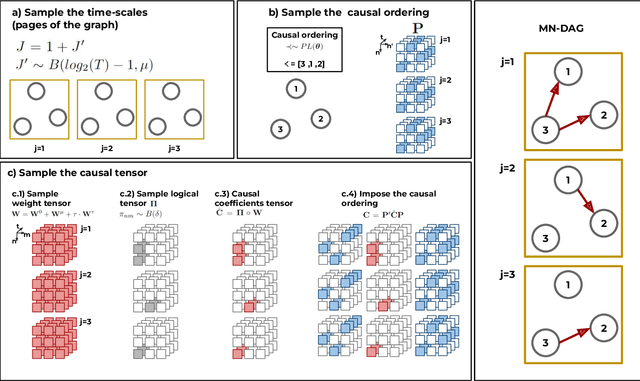
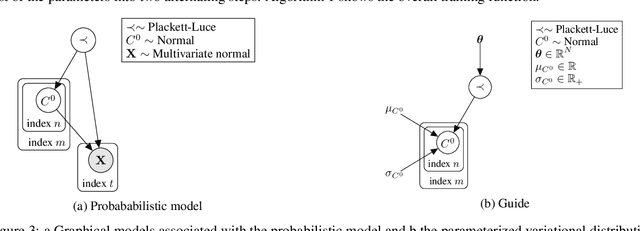
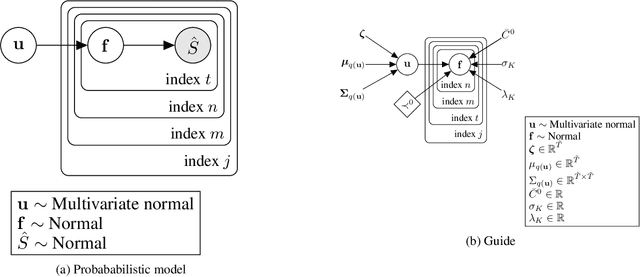
This paper introduces a new type of causal structure, namely multiscale non-stationary directed acyclic graph (MN-DAG), that generalizes DAGs to the time-frequency domain. Our contribution is twofold. First, by leveraging results from spectral and causality theories, we expose a novel probabilistic generative model, which allows to sample an MN-DAG according to user-specified priors concerning the time-dependence and multiscale properties of the causal graph. Second, we devise a Bayesian method for the estimation of MN-DAGs, by means of stochastic variational inference (SVI), called Multiscale Non-Stationary Causal Structure Learner (MN-CASTLE). In addition to direct observations, MN-CASTLE exploits information from the decomposition of the total power spectrum of time series over different time resolutions. In our experiments, we first use the proposed model to generate synthetic data according to a latent MN-DAG, showing that the data generated reproduces well-known features of time series in different domains. Then we compare our learning method MN-CASTLE against baseline models on synthetic data generated with different multiscale and non-stationary settings, confirming the good performance of MN-CASTLE. Finally, we show some insights derived from the application of MN-CASTLE to study the causal structure of 7 global equity markets during the Covid-19 pandemic.

Multiscale Causal Structure Learning

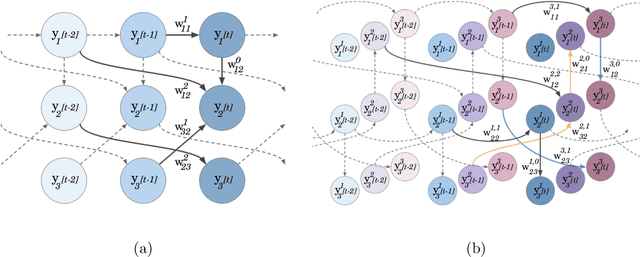
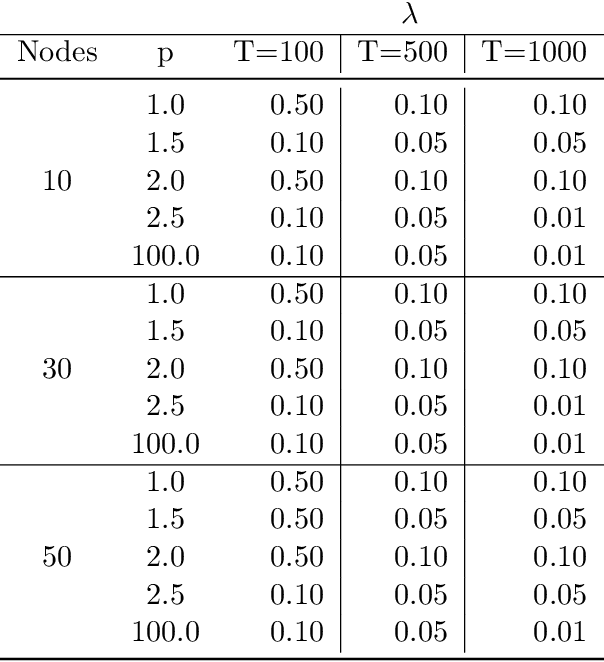
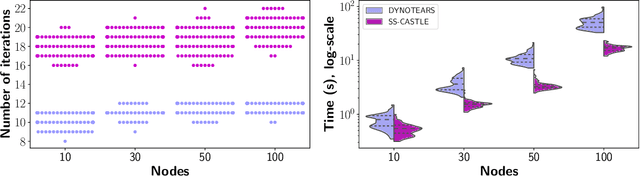
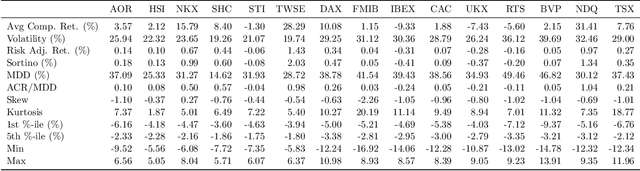
The inference of causal structures from observed data plays a key role in unveiling the underlying dynamics of the system. This paper exposes a novel method, named Multiscale-Causal Structure Learning (MS-CASTLE), to estimate the structure of linear causal relationships occurring at different time scales. Differently from existing approaches, MS-CASTLE takes explicitly into account instantaneous and lagged inter-relations between multiple time series, represented at different scales, hinging on stationary wavelet transform and non-convex optimization. MS-CASTLE incorporates, as a special case, a single-scale version named SS-CASTLE, which compares favorably in terms of computational efficiency, performance and robustness with respect to the state of the art onto synthetic data. We used MS-CASTLE to study the multiscale causal structure of the risk of 15 global equity markets, during covid-19 pandemic, illustrating how MS-CASTLE can extract meaningful information thanks to its multiscale analysis, outperforming SS-CASTLE. We found that the most persistent and strongest interactions occur at mid-term time resolutions. Moreover, we identified the stock markets that drive the risk during the considered period: Brazil, Canada and Italy. The proposed approach can be exploited by financial investors who, depending to their investment horizon, can manage the risk within equity portfolios from a causal perspective.