LLMPC: Large Language Model Predictive Control

Recent advancements in prompting techniques for Large Language Models (LLMs) have improved their reasoning, planning, and action abilities. This paper examines these prompting techniques through the lens of model predictive control (MPC). We show that LLMs act as implicit planning cost function minimizers when planning prompts are used. Under our framework we demonstrate that LLM planning performance can be improved further by incorporating real planning cost functions and evaluators.

A Light-Weight Multi-Objective Asynchronous Hyper-Parameter Optimizer

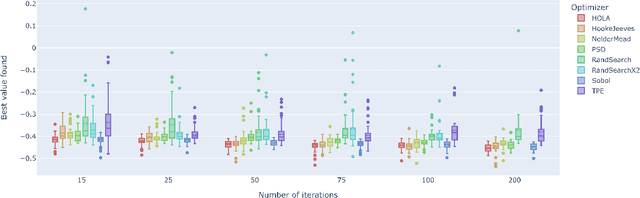
We describe a light-weight yet performant system for hyper-parameter optimization that approximately minimizes an overall scalar cost function that is obtained by combining multiple performance objectives using a target-priority-limit scalarizer. It also supports a trade-off mode, where the goal is to find an appropriate trade-off among objectives by interacting with the user. We focus on the common scenario where there are on the order of tens of hyper-parameters, each with various attributes such as a range of continuous values, or a finite list of values, and whether it should be treated on a linear or logarithmic scale. The system supports multiple asynchronous simulations and is robust to simulation stragglers and failures.

Geometric Uncertainty in Patient-Specific Cardiovascular Modeling with Convolutional Dropout Networks

We propose a novel approach to generate samples from the conditional distribution of patient-specific cardiovascular models given a clinically aquired image volume. A convolutional neural network architecture with dropout layers is first trained for vessel lumen segmentation using a regression approach, to enable Bayesian estimation of vessel lumen surfaces. This network is then integrated into a path-planning patient-specific modeling pipeline to generate families of cardiovascular models. We demonstrate our approach by quantifying the effect of geometric uncertainty on the hemodynamics for three patient-specific anatomies, an aorto-iliac bifurcation, an abdominal aortic aneurysm and a sub-model of the left coronary arteries. A key innovation introduced in the proposed approach is the ability to learn geometric uncertainty directly from training data. The results show how geometric uncertainty produces coefficients of variation comparable to or larger than other sources of uncertainty for wall shear stress and velocity magnitude, but has limited impact on pressure. Specifically, this is true for anatomies characterized by small vessel sizes, and for local vessel lesions seen infrequently during network training.