Mechanism Design With Predictions for Obnoxious Facility Location

We study mechanism design with predictions for the obnoxious facility location problem. We present deterministic strategyproof mechanisms that display tradeoffs between robustness and consistency on segments, squares, circles and trees. All these mechanisms are actually group strategyproof, with the exception of the case of squares, where manipulations from coalitions of two agents exist. We prove that these tradeoffs are optimal in the 1-dimensional case.

Game-Theoretic Models of Moral and Other-Regarding Agents

We investigate Kantian equilibria in finite normal form games, a class of non-Nashian, morally motivated courses of action that was recently proposed in the economics literature. We highlight a number of problems with such equilibria, including computational intractability, a high price of miscoordination, and problematic extension to general normal form games. We give such a generalization based on concept of program equilibria, and point out that that a practically relevant generalization may not exist. To remedy this we propose some general, intuitive, computationally tractable, other-regarding equilibria that are special cases Kantian equilibria, as well as a class of courses of action that interpolates between purely self-regarding and Kantian behavior.

Models we Can Trust: Toward a Systematic Discipline of Model Interpretation and Validation

We advocate the development of a discipline of interacting with and extracting information from models, both mathematical (e.g. game-theoretic ones) and computational (e.g. agent-based models). We outline some directions for the development of a such a discipline: - the development of logical frameworks for the systematic formal specification of stylized facts and social mechanisms in (mathematical and computational) social science. Such frameworks would bring to attention new issues, such as phase transitions, i.e. dramatical changes in the validity of the stylized facts beyond some critical values in parameter space. We argue that such statements are useful for those logical frameworks describing properties of ABM. - the adaptation of tools from the theory of reactive systems (such as bisimulation) to obtain practically relevant notions of two systems "having the same behavior". - the systematic development of an adversarial theory of model perturbations, that investigates the robustness of conclusions derived from models of social behavior to variations in several features of the social dynamics. These may include: activation order, the underlying social network, individual agent behavior.

Game-theoretic Models of Moral and Other-Regarding Agents

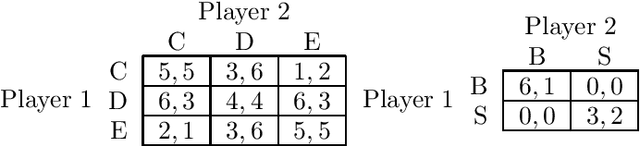
We investigate Kantian equilibria in finite normal form games, a class of non-Nashian, morally motivated courses of action that was recently proposed in the economics literature. We highlight a number of problems with such equilibria, including computational intractability, a high price of miscoordination, and expensive/problematic extension to general normal form games. We point out that such a proper generalization will likely involve the concept of program equilibrium. Finally we propose some general, intuitive, computationally tractable, other-regarding equilibria related to Kantian equilibria, as well as a class of courses of action that interpolates between purely self-regarding and Kantian behavior.

Being Central on the Cheap: Stability in Heterogeneous Multiagent Centrality Games

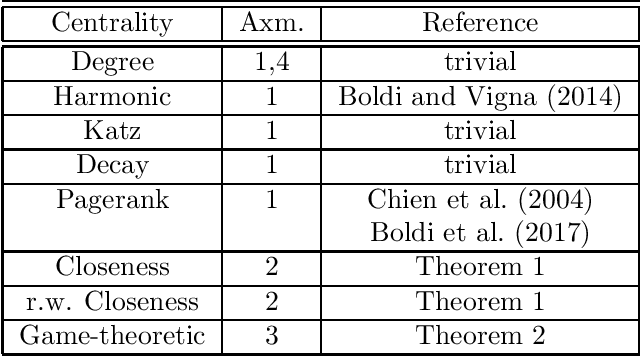
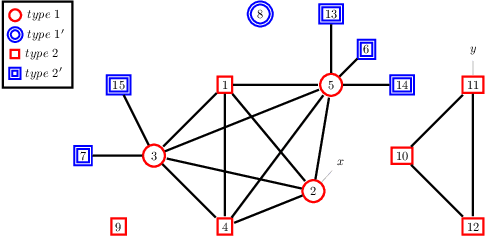
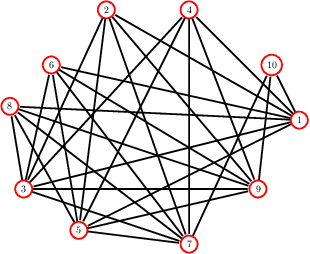
We study strategic network formation games in which agents attempt to form (costly) links in order to maximize their network centrality. Our model derives from Jackson and Wolinsky's symmetric connection model, but allows for heterogeneity in agent utilities by replacing decay centrality (implicit in the Jackson-Wolinsky model) by a variety of classical centrality and game-theoretic measures of centrality. We are primarily interested in characterizing the asymptotically pairwise stable networks, i.e. those networks that are pairwise stable for all sufficiently small, positive edge costs. We uncover a rich typology of stability: - we give an axiomatic approach to network centrality that allows us to predict the stable network for a rich set of combination of centrality utility functions, yielding stable networks with features reminiscent of structural properties such as "core periphery" and "rich club" networks. - We show that a simple variation on the model renders it universal, i.e. every network may be a stable network. - We also show that often we can infer a significant amount about agent utilities from the structure of stable networks.

It's Not Whom You Know, It's What You Can Do: Succint Coalitional Frameworks for Network Centralities

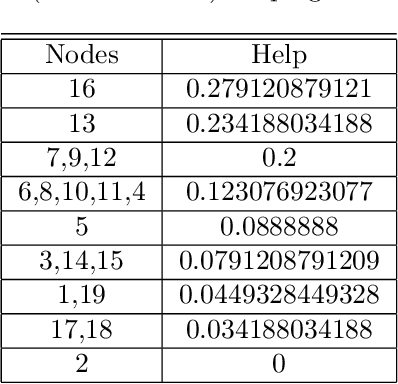
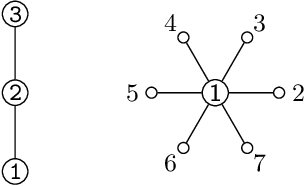
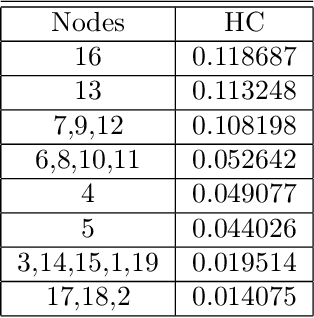
We investigate the representation of measures of network centrality using a framework that blends a social network representation with the succint formalism of cooperative skill games. We discuss the expressiveness of the new framework and highlight some of its advantages, including a fixed-parameter tractability result for computing centrality measures under such representations. As an application we introduce new network centrality measures that capture the extent to which neighbors of a certain node can help it complete relevant tasks.

Attacking Power Indices by Manipulating Player Reliability

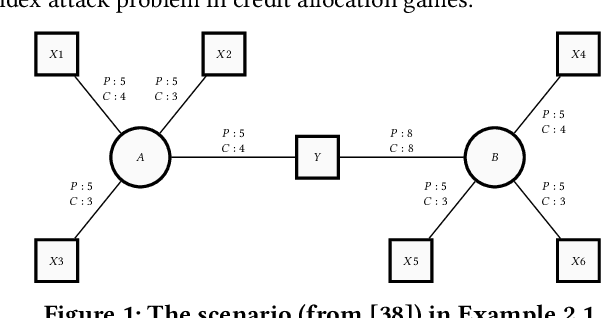
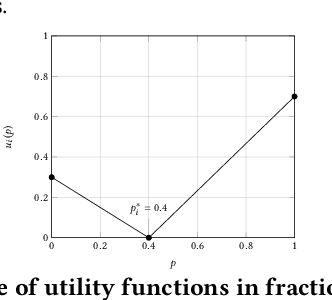
We investigate the manipulation of power indices in TU-cooperative games by stimulating (subject to a budget constraint) changes in the propensity of other players to participate to the game. We display several algorithms that show that the problem is often tractable for so-called network centrality games and influence attribution games, as well as an example when optimal manipulation is intractable, even though computing power indices is feasible.

Spines of Random Constraint Satisfaction Problems: Definition and Connection with Computational Complexity

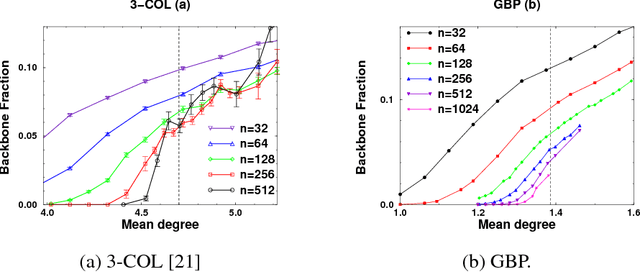
We study the connection between the order of phase transitions in combinatorial problems and the complexity of decision algorithms for such problems. We rigorously show that, for a class of random constraint satisfaction problems, a limited connection between the two phenomena indeed exists. Specifically, we extend the definition of the spine order parameter of Bollobas et al. to random constraint satisfaction problems, rigorously showing that for such problems a discontinuity of the spine is associated with a $2^{\Omega(n)}$ resolution complexity (and thus a $2^{\Omega(n)}$ complexity of DPLL algorithms) on random instances. The two phenomena have a common underlying cause: the emergence of ``large'' (linear size) minimally unsatisfiable subformulas of a random formula at the satisfiability phase transition. We present several further results that add weight to the intuition that random constraint satisfaction problems with a sharp threshold and a continuous spine are ``qualitatively similar to random 2-SAT''. Finally, we argue that it is the spine rather than the backbone parameter whose continuity has implications for the decision complexity of combinatorial problems, and we provide experimental evidence that the two parameters can behave in a different manner.