Deep reinforced learning heuristic tested on spin-glass ground states: The larger picture

In Changjun Fan et al. [Nature Communications https://doi.org/10.1038/s41467-023-36363-w (2023)], the authors present a deep reinforced learning approach to augment combinatorial optimization heuristics. In particular, they present results for several spin glass ground state problems, for which instances on non-planar networks are generally NP-hard, in comparison with several Monte Carlo based methods, such as simulated annealing (SA) or parallel tempering (PT). Indeed, those results demonstrate that the reinforced learning improves the results over those obtained with SA or PT, or at least allows for reduced runtimes for the heuristics before results of comparable quality have been obtained relative to those other methods. To facilitate the conclusion that their method is ''superior'', the authors pursue two basic strategies: (1) A commercial GUROBI solver is called on to procure a sample of exact ground states as a testbed to compare with, and (2) a head-to-head comparison between the heuristics is given for a sample of larger instances where exact ground states are hard to ascertain. Here, we put these studies into a larger context, showing that the claimed superiority is at best marginal for smaller samples and becomes essentially irrelevant with respect to any sensible approximation of true ground states in the larger samples. For example, this method becomes irrelevant as a means to determine stiffness exponents $\theta$ in $d>2$, as mentioned by the authors, where the problem is not only NP-hard but requires the subtraction of two almost equal ground-state energies and systemic errors in each of $\approx 1\%$ found here are unacceptable. This larger picture on the method arises from a straightforward finite-size corrections study over the spin glass ensembles the authors employ, using data that has been available for decades.

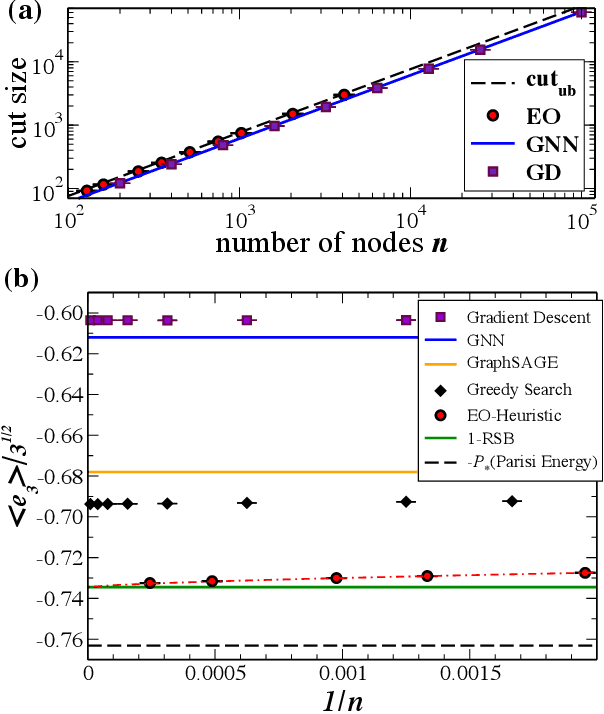
Inability of a graph neural network heuristic to outperform greedy algorithms in solving combinatorial optimization problems like Max-Cut

In Nature Machine Intelligence 4, 367 (2022), Schuetz et al provide a scheme to employ graph neural networks (GNN) as a heuristic to solve a variety of classical, NP-hard combinatorial optimization problems. It describes how the network is trained on sample instances and the resulting GNN heuristic is evaluated applying widely used techniques to determine its ability to succeed. Clearly, the idea of harnessing the powerful abilities of such networks to ``learn'' the intricacies of complex, multimodal energy landscapes in such a hands-off approach seems enticing. And based on the observed performance, the heuristic promises to be highly scalable, with a computational cost linear in the input size $n$, although there is likely a significant overhead in the pre-factor due to the GNN itself. However, closer inspection shows that the reported results for this GNN are only minutely better than those for gradient descent and get outperformed by a greedy algorithm, for example, for Max-Cut. The discussion also highlights what I believe are some common misconceptions in the evaluations of heuristics.

Spines of Random Constraint Satisfaction Problems: Definition and Connection with Computational Complexity

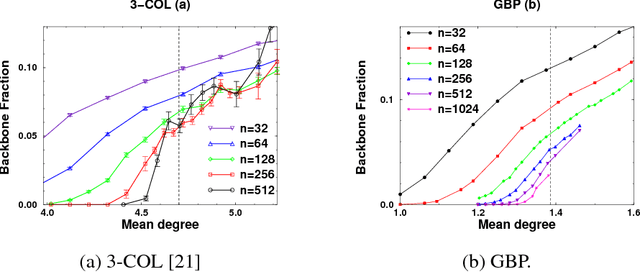
We study the connection between the order of phase transitions in combinatorial problems and the complexity of decision algorithms for such problems. We rigorously show that, for a class of random constraint satisfaction problems, a limited connection between the two phenomena indeed exists. Specifically, we extend the definition of the spine order parameter of Bollobas et al. to random constraint satisfaction problems, rigorously showing that for such problems a discontinuity of the spine is associated with a $2^{\Omega(n)}$ resolution complexity (and thus a $2^{\Omega(n)}$ complexity of DPLL algorithms) on random instances. The two phenomena have a common underlying cause: the emergence of ``large'' (linear size) minimally unsatisfiable subformulas of a random formula at the satisfiability phase transition. We present several further results that add weight to the intuition that random constraint satisfaction problems with a sharp threshold and a continuous spine are ``qualitatively similar to random 2-SAT''. Finally, we argue that it is the spine rather than the backbone parameter whose continuity has implications for the decision complexity of combinatorial problems, and we provide experimental evidence that the two parameters can behave in a different manner.

Extremal Optimization: an Evolutionary Local-Search Algorithm

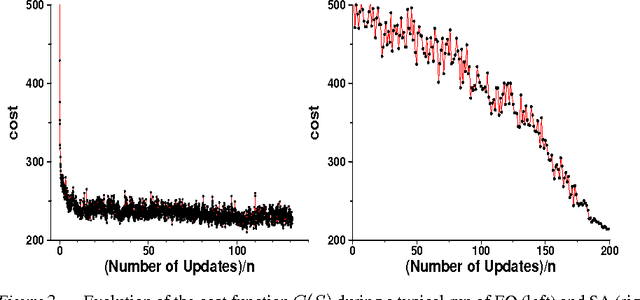
A recently introduced general-purpose heuristic for finding high-quality solutions for many hard optimization problems is reviewed. The method is inspired by recent progress in understanding far-from-equilibrium phenomena in terms of {\em self-organized criticality,} a concept introduced to describe emergent complexity in physical systems. This method, called {\em extremal optimization,} successively replaces the value of extremely undesirable variables in a sub-optimal solution with new, random ones. Large, avalanche-like fluctuations in the cost function self-organize from this dynamics, effectively scaling barriers to explore local optima in distant neighborhoods of the configuration space while eliminating the need to tune parameters. Drawing upon models used to simulate the dynamics of granular media, evolution, or geology, extremal optimization complements approximation methods inspired by equilibrium statistical physics, such as {\em simulated annealing}. It may be but one example of applying new insights into {\em non-equilibrium phenomena} systematically to hard optimization problems. This method is widely applicable and so far has proved competitive with -- and even superior to -- more elaborate general-purpose heuristics on testbeds of constrained optimization problems with up to $10^5$ variables, such as bipartitioning, coloring, and satisfiability. Analysis of a suitable model predicts the only free parameter of the method in accordance with all experimental results.