Spines of Random Constraint Satisfaction Problems: Definition and Connection with Computational Complexity
Paper and Code
Mar 29, 2005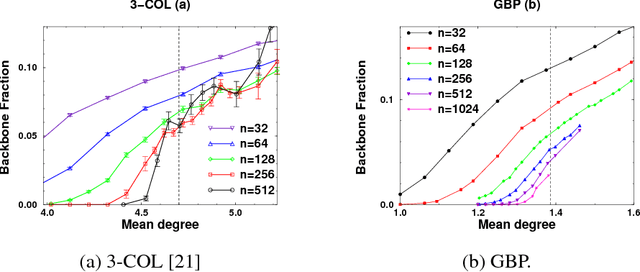
We study the connection between the order of phase transitions in combinatorial problems and the complexity of decision algorithms for such problems. We rigorously show that, for a class of random constraint satisfaction problems, a limited connection between the two phenomena indeed exists. Specifically, we extend the definition of the spine order parameter of Bollobas et al. to random constraint satisfaction problems, rigorously showing that for such problems a discontinuity of the spine is associated with a $2^{\Omega(n)}$ resolution complexity (and thus a $2^{\Omega(n)}$ complexity of DPLL algorithms) on random instances. The two phenomena have a common underlying cause: the emergence of ``large'' (linear size) minimally unsatisfiable subformulas of a random formula at the satisfiability phase transition. We present several further results that add weight to the intuition that random constraint satisfaction problems with a sharp threshold and a continuous spine are ``qualitatively similar to random 2-SAT''. Finally, we argue that it is the spine rather than the backbone parameter whose continuity has implications for the decision complexity of combinatorial problems, and we provide experimental evidence that the two parameters can behave in a different manner.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge