Being Central on the Cheap: Stability in Heterogeneous Multiagent Centrality Games
Paper and Code
Nov 26, 2020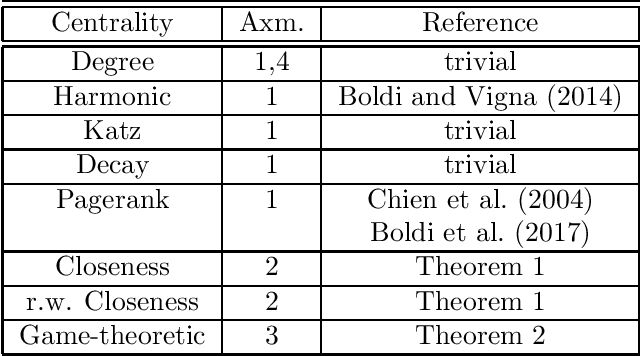
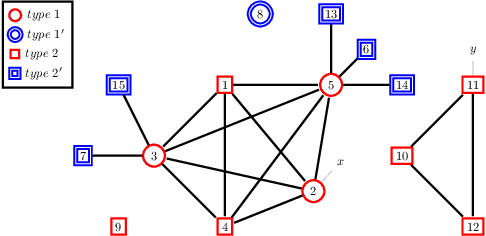
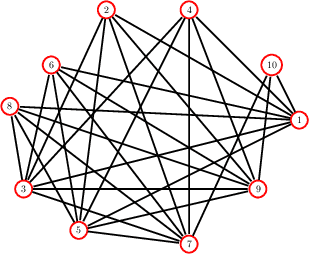
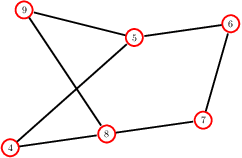
We study strategic network formation games in which agents attempt to form (costly) links in order to maximize their network centrality. Our model derives from Jackson and Wolinsky's symmetric connection model, but allows for heterogeneity in agent utilities by replacing decay centrality (implicit in the Jackson-Wolinsky model) by a variety of classical centrality and game-theoretic measures of centrality. We are primarily interested in characterizing the asymptotically pairwise stable networks, i.e. those networks that are pairwise stable for all sufficiently small, positive edge costs. We uncover a rich typology of stability: - we give an axiomatic approach to network centrality that allows us to predict the stable network for a rich set of combination of centrality utility functions, yielding stable networks with features reminiscent of structural properties such as "core periphery" and "rich club" networks. - We show that a simple variation on the model renders it universal, i.e. every network may be a stable network. - We also show that often we can infer a significant amount about agent utilities from the structure of stable networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge