Gábor Braun
Lazifying Conditional Gradient Algorithms
Sep 05, 2018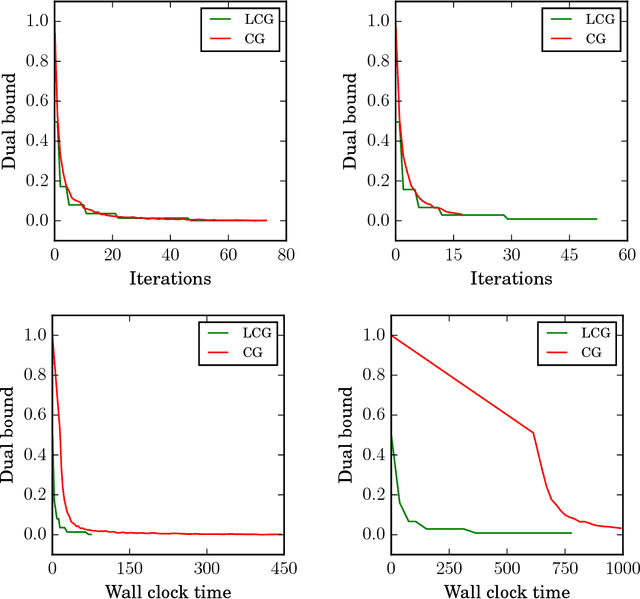
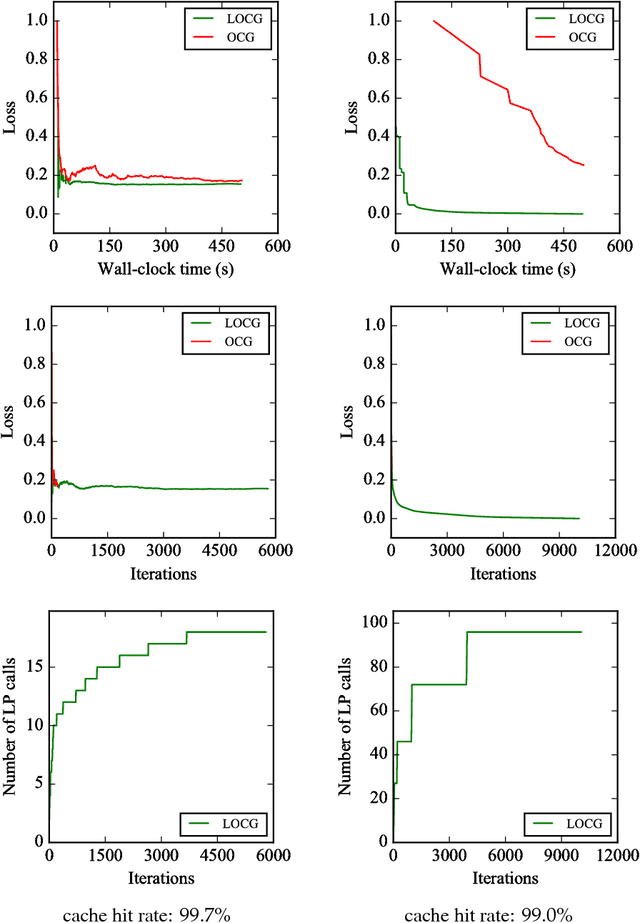
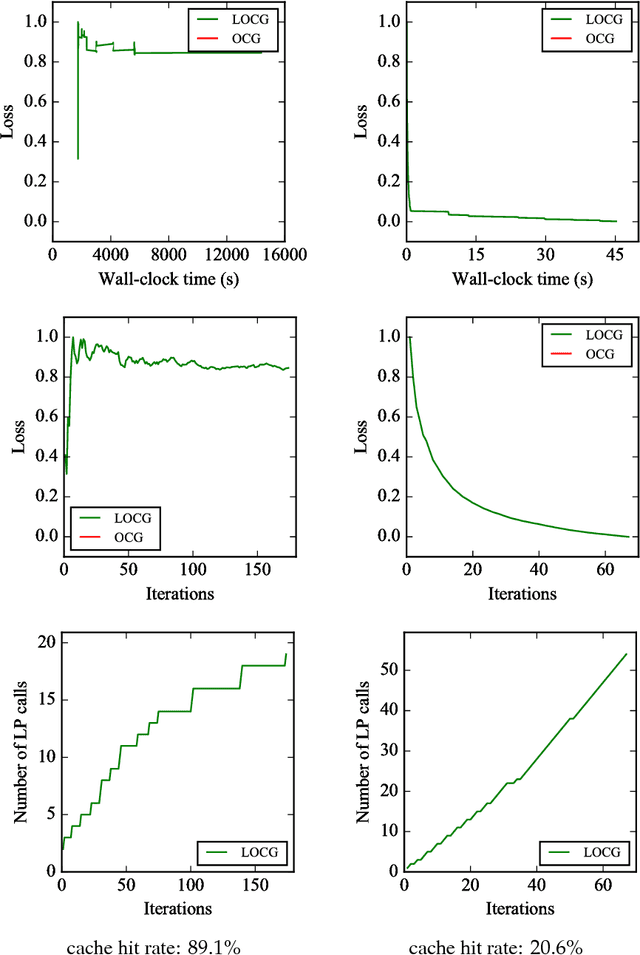
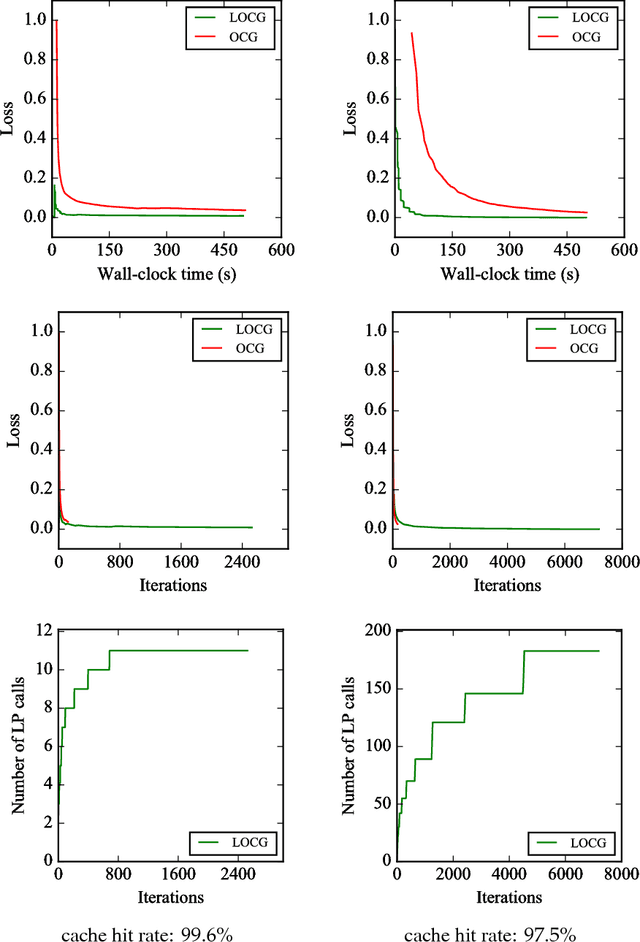
Abstract:Conditional gradient algorithms (also often called Frank-Wolfe algorithms) are popular due to their simplicity of only requiring a linear optimization oracle and more recently they also gained significant traction for online learning. While simple in principle, in many cases the actual implementation of the linear optimization oracle is costly. We show a general method to lazify various conditional gradient algorithms, which in actual computations leads to several orders of magnitude of speedup in wall-clock time. This is achieved by using a faster separation oracle instead of a linear optimization oracle, relying only on few linear optimization oracle calls.
Blended Conditional Gradients: the unconditioning of conditional gradients
May 18, 2018
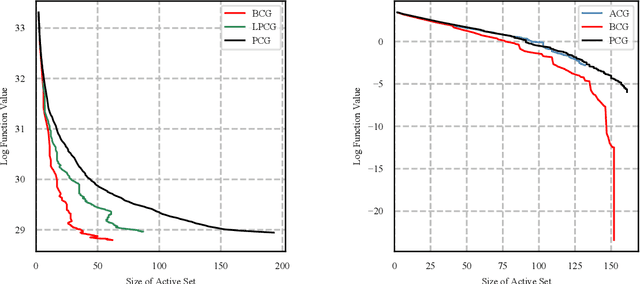
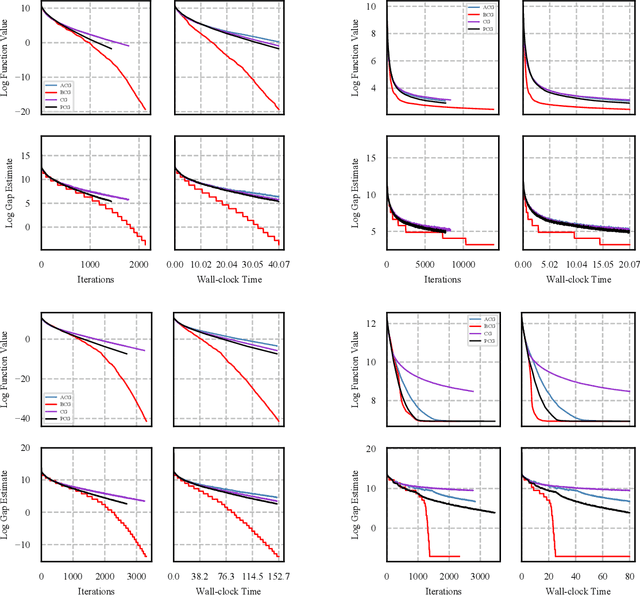
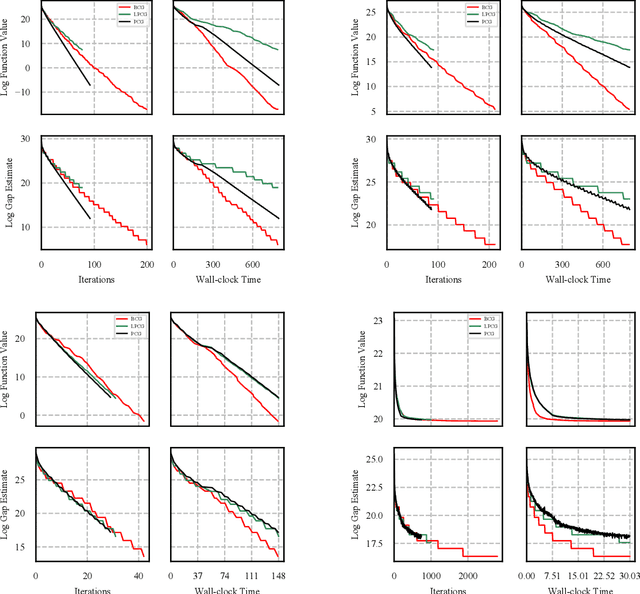
Abstract:We present a blended conditional gradient approach for minimizing a smooth convex function over a polytope $P$, that combines the Frank--Wolfe algorithm (also called conditional gradient) with gradient-based steps different from away steps and pairwise steps, however, still achieving linear convergence for strongly convex functions and good practical performance. Our approach retains all favorable properties of conditional gradient algorithms, most notably avoidance of projections onto $P$ and maintenance of iterates as sparse convex combinations of a limited number of extreme points of $P$. The algorithm decreases measures of optimality (primal and dual gaps) rapidly, both in the number of iterations and in wall-clock time, outperforming even the efficient "lazified" conditional gradient algorithms of [arXiv:1410.8816]. Nota bene the algorithm is lazified itself. We also present a streamlined algorithm when $P$ is the probability simplex.
An efficient high-probability algorithm for Linear Bandits
Oct 13, 2016Abstract:For the linear bandit problem, we extend the analysis of algorithm CombEXP from [R. Combes, M. S. Talebi Mazraeh Shahi, A. Proutiere, and M. Lelarge. Combinatorial bandits revisited. In C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, and R. Garnett, editors, Advances in Neural Information Processing Systems 28, pages 2116--2124. Curran Associates, Inc., 2015. URL http://papers.nips.cc/paper/5831-combinatorial-bandits-revisited.pdf] to the high-probability case against adaptive adversaries, allowing actions to come from an arbitrary polytope. We prove a high-probability regret of \(O(T^{2/3})\) for time horizon \(T\). While this bound is weaker than the optimal \(O(\sqrt{T})\) bound achieved by GeometricHedge in [P. L. Bartlett, V. Dani, T. Hayes, S. Kakade, A. Rakhlin, and A. Tewari. High-probability regret bounds for bandit online linear optimization. In 21th Annual Conference on Learning Theory (COLT 2008), July 2008. http://eprints.qut.edu.au/45706/1/30-Bartlett.pdf], CombEXP is computationally efficient, requiring only an efficient linear optimization oracle over the convex hull of the actions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge