Blended Conditional Gradients: the unconditioning of conditional gradients

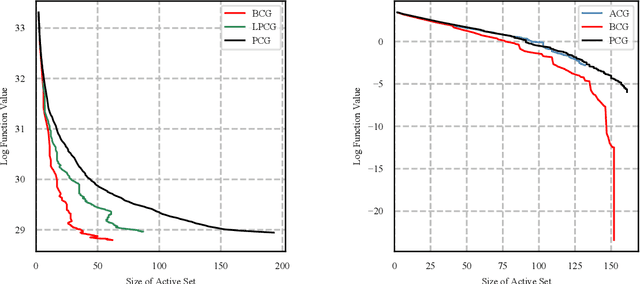
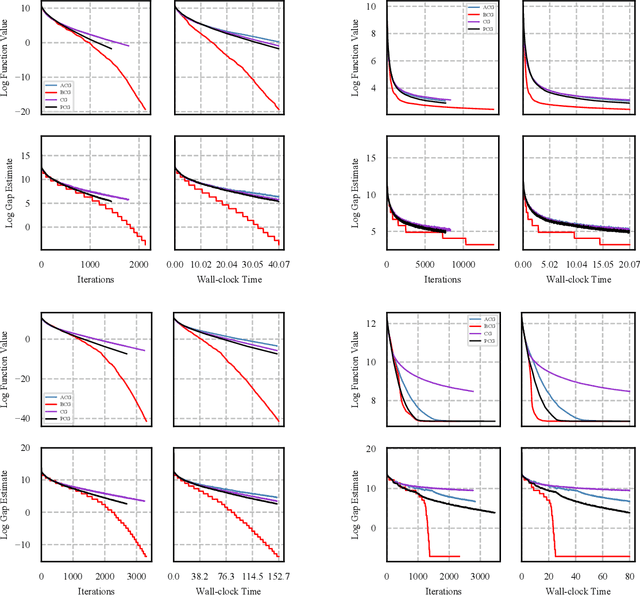
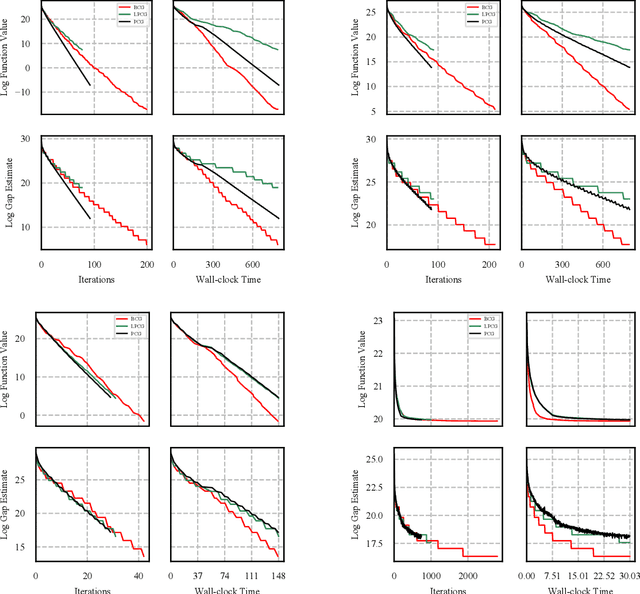
We present a blended conditional gradient approach for minimizing a smooth convex function over a polytope $P$, that combines the Frank--Wolfe algorithm (also called conditional gradient) with gradient-based steps different from away steps and pairwise steps, however, still achieving linear convergence for strongly convex functions and good practical performance. Our approach retains all favorable properties of conditional gradient algorithms, most notably avoidance of projections onto $P$ and maintenance of iterates as sparse convex combinations of a limited number of extreme points of $P$. The algorithm decreases measures of optimality (primal and dual gaps) rapidly, both in the number of iterations and in wall-clock time, outperforming even the efficient "lazified" conditional gradient algorithms of [arXiv:1410.8816]. Nota bene the algorithm is lazified itself. We also present a streamlined algorithm when $P$ is the probability simplex.