Daniel Zink
Lazifying Conditional Gradient Algorithms
Sep 05, 2018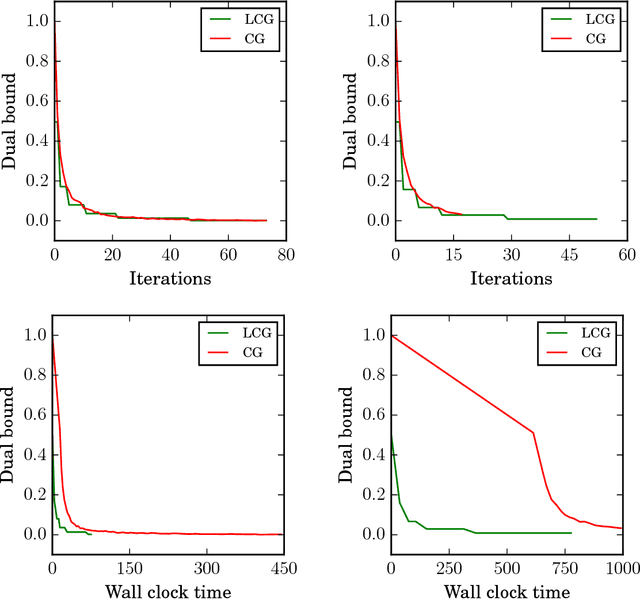
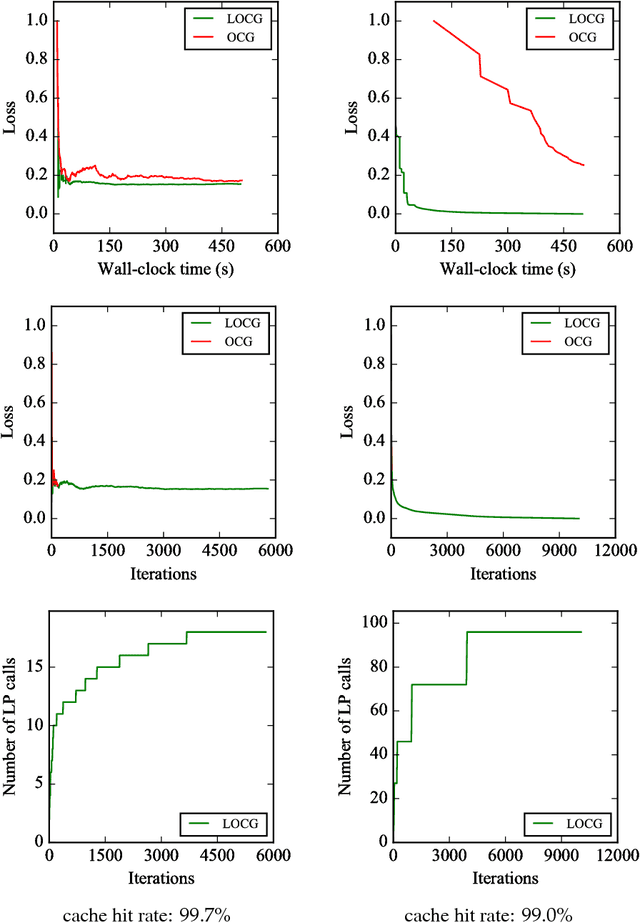
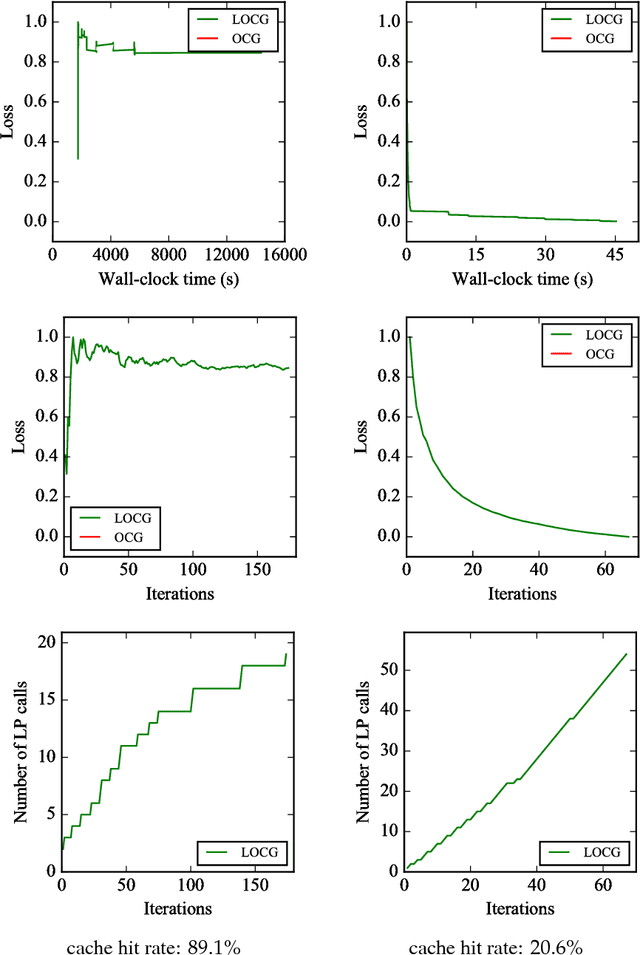
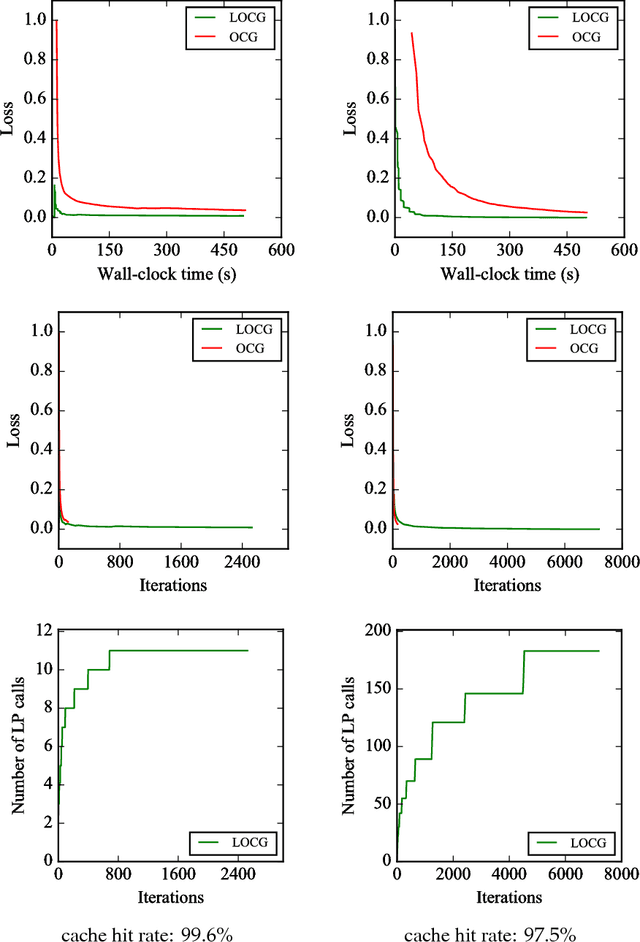
Abstract:Conditional gradient algorithms (also often called Frank-Wolfe algorithms) are popular due to their simplicity of only requiring a linear optimization oracle and more recently they also gained significant traction for online learning. While simple in principle, in many cases the actual implementation of the linear optimization oracle is costly. We show a general method to lazify various conditional gradient algorithms, which in actual computations leads to several orders of magnitude of speedup in wall-clock time. This is achieved by using a faster separation oracle instead of a linear optimization oracle, relying only on few linear optimization oracle calls.
Conditional Accelerated Lazy Stochastic Gradient Descent
Feb 15, 2018



Abstract:In this work we introduce a conditional accelerated lazy stochastic gradient descent algorithm with optimal number of calls to a stochastic first-order oracle and convergence rate $O\left(\frac{1}{\varepsilon^2}\right)$ improving over the projection-free, Online Frank-Wolfe based stochastic gradient descent of Hazan and Kale [2012] with convergence rate $O\left(\frac{1}{\varepsilon^4}\right)$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge