How Does Unfaithful Reasoning Emerge from Autoregressive Training? A Study of Synthetic Experiments

Chain-of-thought (CoT) reasoning generated by large language models (LLMs) is often unfaithful: intermediate steps can be logically inconsistent or fail to reflect the causal relationship leading to the final answer. Despite extensive empirical observations, a fundamental understanding of CoT is lacking--what constitutes faithful CoT reasoning, and how unfaithfulness emerges from autoregressive training. We study these questions using well-controlled synthetic experiments, training small transformers on noisy data to solve modular arithmetic expressions step by step, a task we term Arithmetic Expression Reasoning. We find that models can learn faithful reasoning that causally follows the underlying arithmetic rules, but only when the training noise is below a critical threshold, a phenomenon attributable to simplicity bias. At higher noise levels, training dynamics exhibit a transition from faithful stepwise reasoning to unfaithful skip-step reasoning via an intermediate mixed mode characterized by a transient increase in prediction entropy. Mechanistic analysis reveals that models learn to encode internal uncertainty by resolving inconsistent reasoning steps, which suggests the emergence of implicit self-verification from autoregressive training.

Low Cost Edge Sensing for High Quality Demosaicking

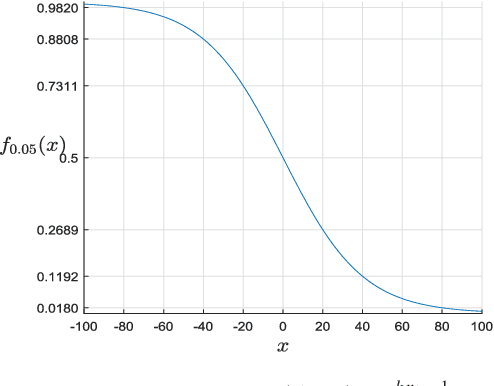
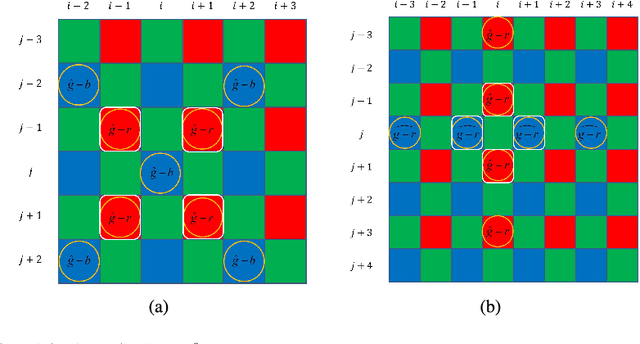
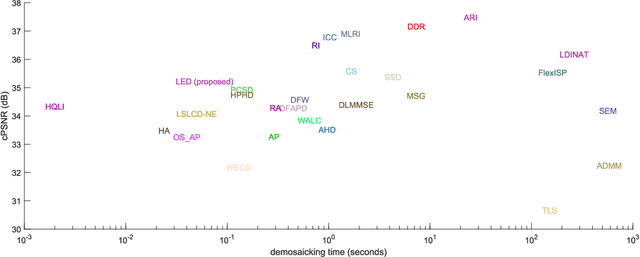
Digital cameras that use Color Filter Arrays (CFA) entail a demosaicking procedure to form full RGB images. As today's camera users generally require images to be viewed instantly, demosaicking algorithms for real applications must be fast. Moreover, the associated cost should be lower than the cost saved by using CFA. For this purpose, we revisit the classical Hamilton-Adams (HA) algorithm, which outperforms many sophisticated techniques in both speed and accuracy. Inspired by HA's strength and weakness, we design a very low cost edge sensing scheme. Briefly, it guides demosaicking by a logistic functional of the difference between directional variations. We extensively compare our algorithm with 28 demosaicking algorithms by running their open source codes on benchmark datasets. Compared to methods of similar computational cost, our method achieves substantially higher accuracy, Whereas compared to methods of similar accuracy, our method has significantly lower cost. Moreover, on test images of currently popular resolution, the quality of our algorithm is comparable to top performers, whereas its speed is tens of times faster.