Robust and integrative Bayesian neural networks for likelihood-free parameter inference

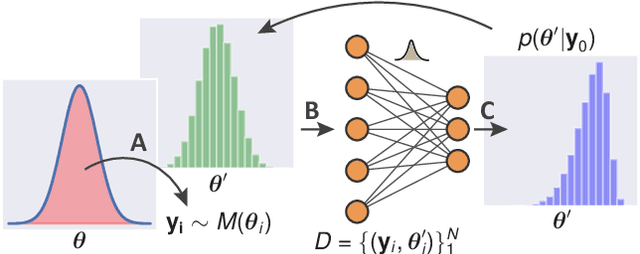
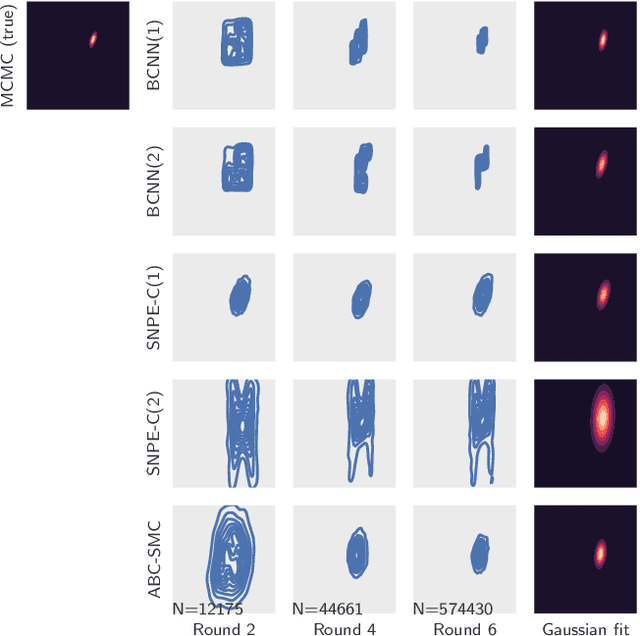
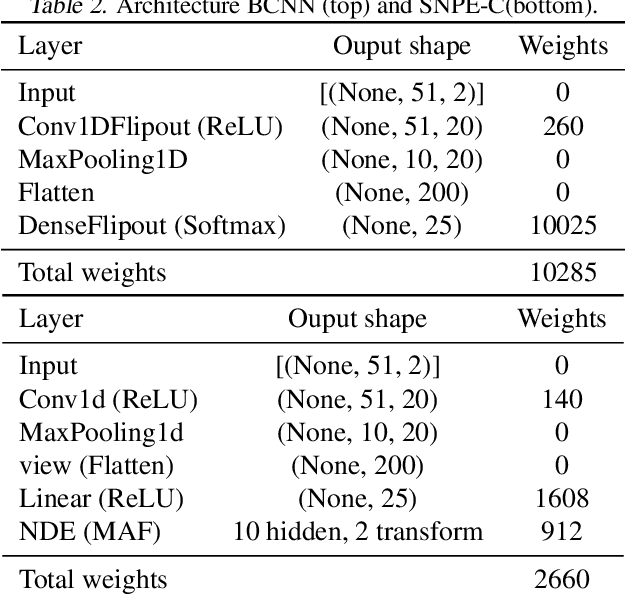
State-of-the-art neural network-based methods for learning summary statistics have delivered promising results for simulation-based likelihood-free parameter inference. Existing approaches require density estimation as a post-processing step building upon deterministic neural networks, and do not take network prediction uncertainty into account. This work proposes a robust integrated approach that learns summary statistics using Bayesian neural networks, and directly estimates the posterior density using categorical distributions. An adaptive sampling scheme selects simulation locations to efficiently and iteratively refine the predictive posterior of the network conditioned on observations. This allows for more efficient and robust convergence on comparatively large prior spaces. We demonstrate our approach on benchmark examples and compare against related methods.

Convolutional Neural Networks as Summary Statistics for Approximate Bayesian Computation

Approximate Bayesian Computation is widely used in systems biology for inferring parameters in stochastic gene regulatory network models. Its performance hinges critically on the ability to summarize high-dimensional system responses such as time series into a few informative, low-dimensional summary statistics. The quality of those statistics critically affect the accuracy of the inference. Existing methods to select the best subset out of a pool of candidate statistics do not scale well with large pools. Since it is imperative for good performance this becomes a serious bottleneck when doing inference on complex and high-dimensional problems. This paper proposes a convolutional neural network architecture for automatically learning informative summary statistics of temporal responses. We show that the proposed network can effectively circumvent the statistics selection problem as a preprocessing step to ABC for a challenging inference problem learning parameters in a high-dimensional stochastic genetic oscillator. We also study the impact of experimental design on network performance by comparing different data richness and different data acquisition strategies.