Learning Variational Data Assimilation Models and Solvers

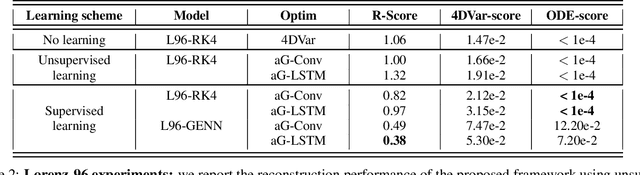
This paper addresses variational data assimilation from a learning point of view. Data assimilation aims to reconstruct the time evolution of some state given a series of observations, possibly noisy and irregularly-sampled. Using automatic differentiation tools embedded in deep learning frameworks, we introduce end-to-end neural network architectures for data assimilation. It comprises two key components: a variational model and a gradient-based solver both implemented as neural networks. A key feature of the proposed end-to-end learning architecture is that we may train the NN models using both supervised and unsupervised strategies. Our numerical experiments on Lorenz-63 and Lorenz-96 systems report significant gain w.r.t. a classic gradient-based minimization of the variational cost both in terms of reconstruction performance and optimization complexity. Intriguingly, we also show that the variational models issued from the true Lorenz-63 and Lorenz-96 ODE representations may not lead to the best reconstruction performance. We believe these results may open new research avenues for the specification of assimilation models in geoscience.

Joint learning of variational representations and solvers for inverse problems with partially-observed data

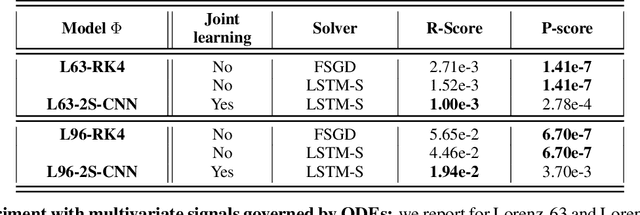
Designing appropriate variational regularization schemes is a crucial part of solving inverse problems, making them better-posed and guaranteeing that the solution of the associated optimization problem satisfies desirable properties. Recently, learning-based strategies have appeared to be very efficient for solving inverse problems, by learning direct inversion schemes or plug-and-play regularizers from available pairs of true states and observations. In this paper, we go a step further and design an end-to-end framework allowing to learn actual variational frameworks for inverse problems in such a supervised setting. The variational cost and the gradient-based solver are both stated as neural networks using automatic differentiation for the latter. We can jointly learn both components to minimize the data reconstruction error on the true states. This leads to a data-driven discovery of variational models. We consider an application to inverse problems with incomplete datasets (image inpainting and multivariate time series interpolation). We experimentally illustrate that this framework can lead to a significant gain in terms of reconstruction performance, including w.r.t. the direct minimization of the variational formulation derived from the known generative model.

Residual Networks as Geodesic Flows of Diffeomorphisms

This paper addresses the understanding and characterization of residual networks (ResNet), which are among the state-of-the-art deep learning architectures for a variety of supervised learning problems. We focus on the mapping component of ResNets, which map the embedding space towards a new unknown space where the prediction or classification can be stated according to linear criteria. We show that this mapping component can be regarded as the numerical implementation of continuous flows of diffeomorphisms governed by ordinary differential equations. Especially, ResNets with shared weights are fully characterized as numerical approximation of exponential diffeomorphic operators. We stress both theoretically and numerically the relevance of the enforcement of diffeormorphic properties and the importance of numerical issues to make consistent the continuous formulation and the discretized ResNet implementation. We further discuss the resulting theoretical and computational insights on ResNet architectures.