Ensemble forecasts in reproducing kernel Hilbert space family: dynamical systems in Wonderland

A methodological framework for ensemble-based estimation and simulation of high dimensional dynamical systems such as the oceanic or atmospheric flows is proposed. To that end, the dynamical system is embedded in a family of reproducing kernel Hilbert spaces with kernel functions driven by the dynamics. This family is nicknamed Wonderland for its appealing properties. In Wonderland the Koopman and Perron-Frobenius operators are unitary and uniformly continuous. This property warrants they can be expressed in exponential series of diagonalizable bounded infinitesimal generators. Access to Lyapunov exponents and to exact ensemble based expressions of the tangent linear dynamics are directly available as well. Wonderland enables us the devise of strikingly simple ensemble data assimilation methods for trajectory reconstructions in terms of constant-in-time linear combinations of trajectory samples. Such an embarrassingly simple strategy is made possible through a fully justified superposition principle ensuing from several fundamental theorems.

Learning Variational Data Assimilation Models and Solvers

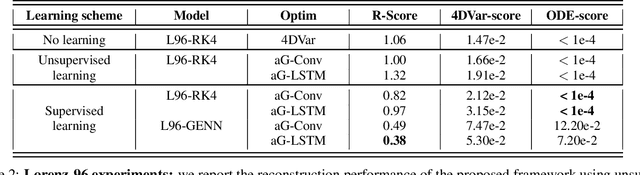
This paper addresses variational data assimilation from a learning point of view. Data assimilation aims to reconstruct the time evolution of some state given a series of observations, possibly noisy and irregularly-sampled. Using automatic differentiation tools embedded in deep learning frameworks, we introduce end-to-end neural network architectures for data assimilation. It comprises two key components: a variational model and a gradient-based solver both implemented as neural networks. A key feature of the proposed end-to-end learning architecture is that we may train the NN models using both supervised and unsupervised strategies. Our numerical experiments on Lorenz-63 and Lorenz-96 systems report significant gain w.r.t. a classic gradient-based minimization of the variational cost both in terms of reconstruction performance and optimization complexity. Intriguingly, we also show that the variational models issued from the true Lorenz-63 and Lorenz-96 ODE representations may not lead to the best reconstruction performance. We believe these results may open new research avenues for the specification of assimilation models in geoscience.