Residual Networks as Geodesic Flows of Diffeomorphisms
Paper and Code
Jun 22, 2018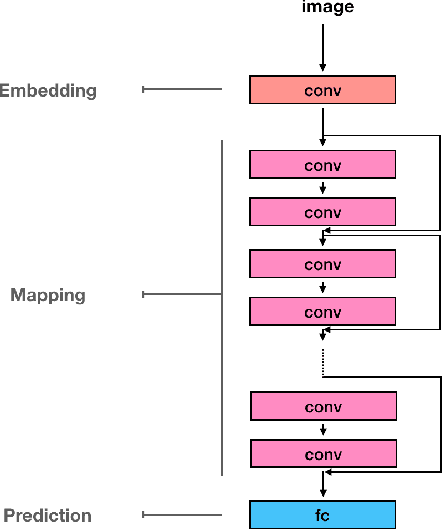
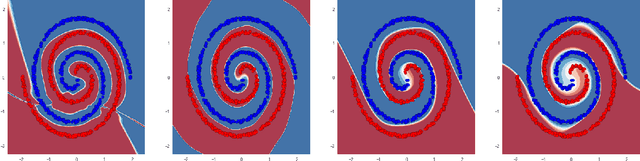
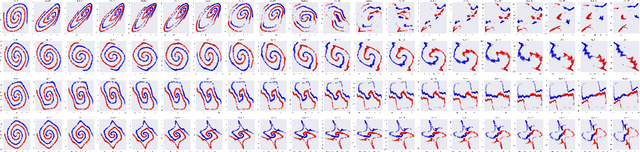
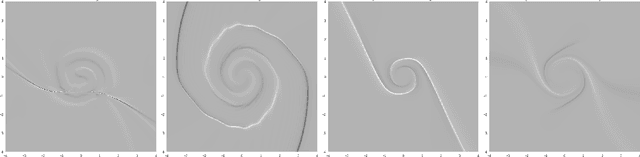
This paper addresses the understanding and characterization of residual networks (ResNet), which are among the state-of-the-art deep learning architectures for a variety of supervised learning problems. We focus on the mapping component of ResNets, which map the embedding space towards a new unknown space where the prediction or classification can be stated according to linear criteria. We show that this mapping component can be regarded as the numerical implementation of continuous flows of diffeomorphisms governed by ordinary differential equations. Especially, ResNets with shared weights are fully characterized as numerical approximation of exponential diffeomorphic operators. We stress both theoretically and numerically the relevance of the enforcement of diffeormorphic properties and the importance of numerical issues to make consistent the continuous formulation and the discretized ResNet implementation. We further discuss the resulting theoretical and computational insights on ResNet architectures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge