Coulomb Autoencoders

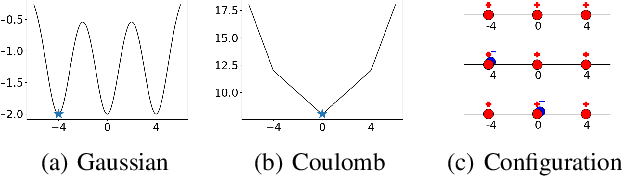
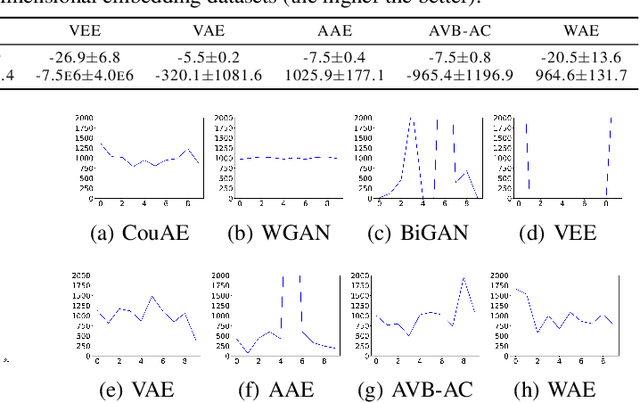
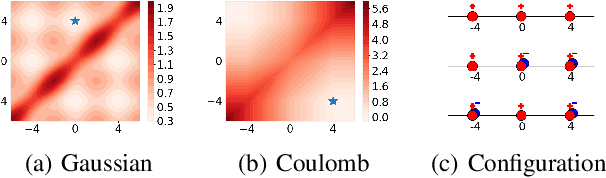
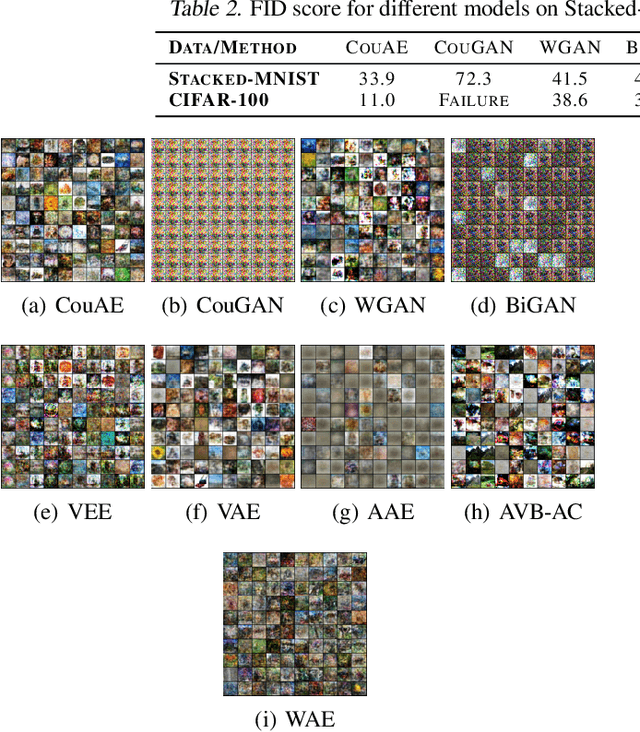
Estimating the true density in high-dimensional feature spaces is a well-known problem in machine learning. We propose a new implicit generative model based on autoencoders, whose training is guaranteed to converge to the global minimum of the objective function. This is achieved by using an appropriate family of kernel functions in the regularizer. Furthermore, we analyze the behaviour of the proposed model in the case of finite number of samples and provide an upper bound on the generalization error achieved by this global minimum. The theory is corroborated by extensive experimental comparisons on synthetic and real-world datasets against several approaches from the families of generative adversarial networks and autoencoder-based models.

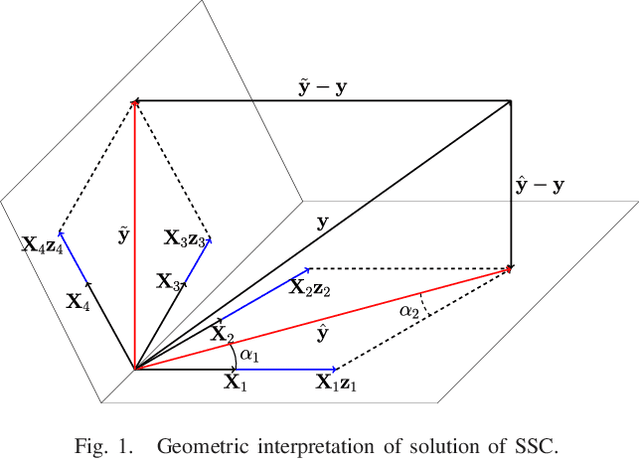
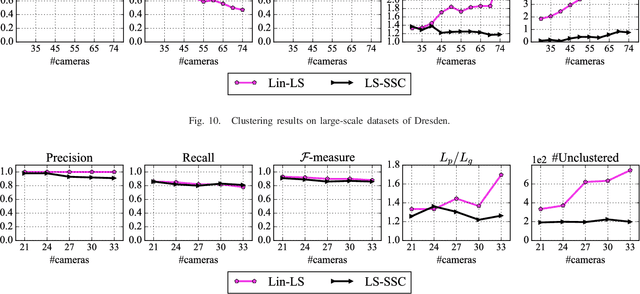
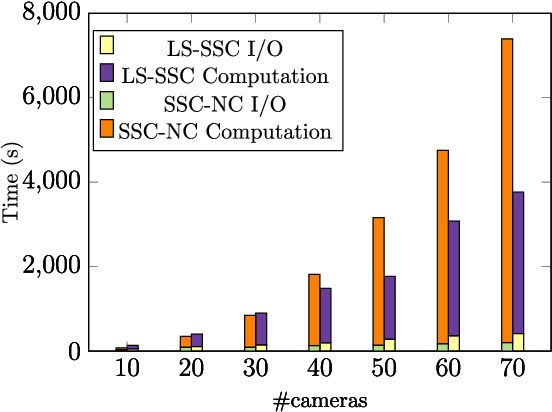
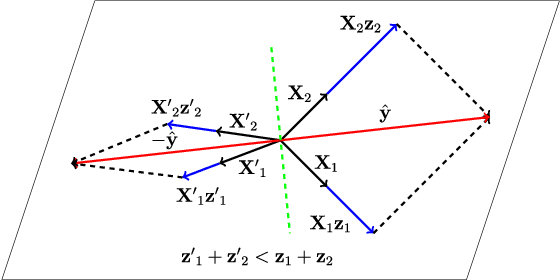
Accurate and Scalable Image Clustering Based On Sparse Representation of Camera Fingerprint

Clustering images according to their acquisition devices is a well-known problem in multimedia forensics, which is typically faced by means of camera Sensor Pattern Noise (SPN). Such an issue is challenging since SPN is a noise-like signal, hard to be estimated and easy to be attenuated or destroyed by many factors. Moreover, the high dimensionality of SPN hinders large-scale applications. Existing approaches are typically based on the correlation among SPNs in the pixel domain, which might not be able to capture intrinsic data structure in union of vector subspaces. In this paper, we propose an accurate clustering framework, which exploits linear dependencies among SPNs in their intrinsic vector subspaces. Such dependencies are encoded under sparse representations which are obtained by solving a Lasso problem with non-negativity constraint. The proposed framework is highly accurate in number of clusters estimation and fingerprint association. Moreover, our framework is scalable to the number of images and robust against double JPEG compression as well as the presence of outliers, owning big potential for real-world applications. Experimental results on Dresden and Vision database show that our proposed framework can adapt well to both medium-scale and large-scale contexts, and outperforms state-of-the-art methods.

Efficient Training for Positive Unlabeled Learning

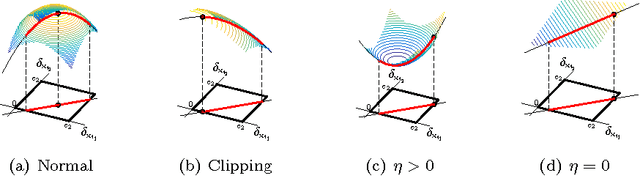
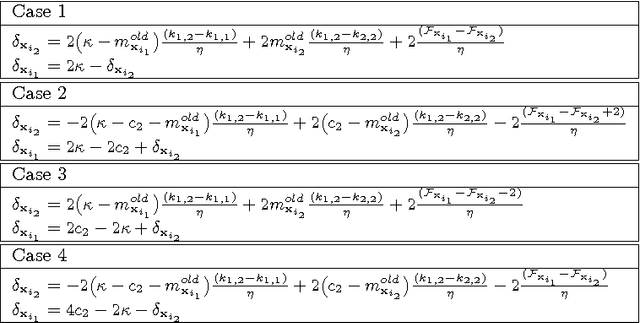
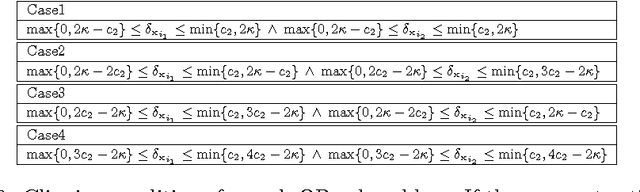
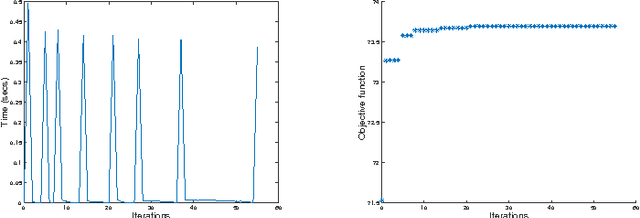
Positive unlabeled (PU) learning is useful in various practical situations, where there is a need to learn a classifier for a class of interest from an unlabeled data set, which may contain anomalies as well as samples from unknown classes. The learning task can be formulated as an optimization problem under the framework of statistical learning theory. Recent studies have theoretically analyzed its properties and generalization performance, nevertheless, little effort has been made to consider the problem of scalability, especially when large sets of unlabeled data are available. In this work we propose a novel scalable PU learning algorithm that is theoretically proven to provide the optimal solution, while showing superior computational and memory performance. Experimental evaluation confirms the theoretical evidence and shows that the proposed method can be successfully applied to a large variety of real-world problems involving PU learning.

Training Feedforward Neural Networks with Standard Logistic Activations is Feasible

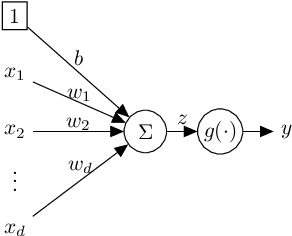
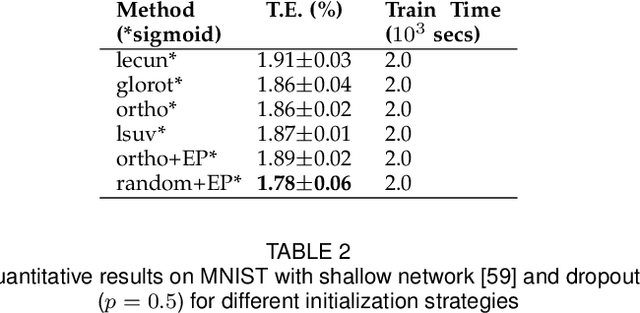
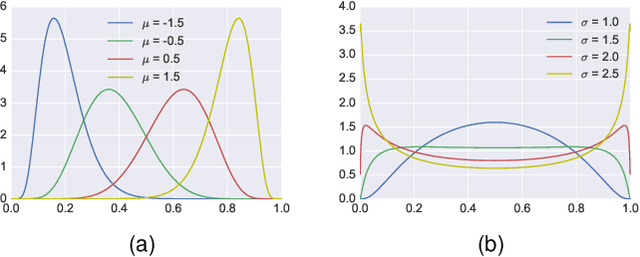
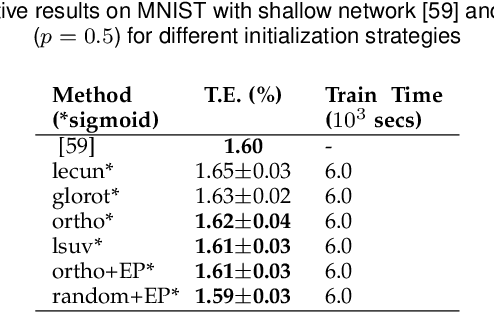
Training feedforward neural networks with standard logistic activations is considered difficult because of the intrinsic properties of these sigmoidal functions. This work aims at showing that these networks can be trained to achieve generalization performance comparable to those based on hyperbolic tangent activations. The solution consists on applying a set of conditions in parameter initialization, which have been derived from the study of the properties of a single neuron from an information-theoretic perspective. The proposed initialization is validated through an extensive experimental analysis.