Coulomb Autoencoders

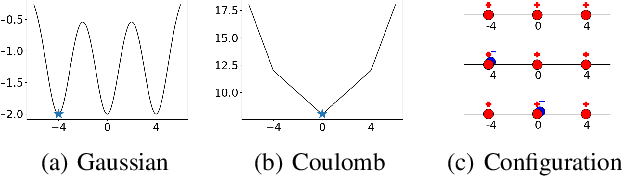
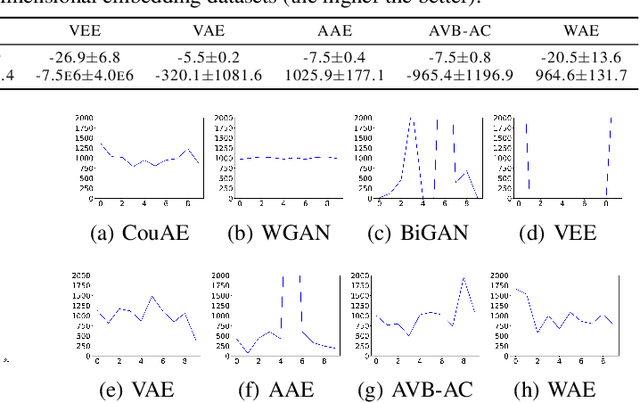
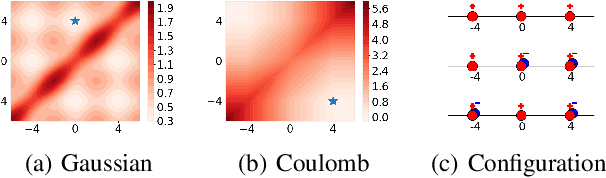
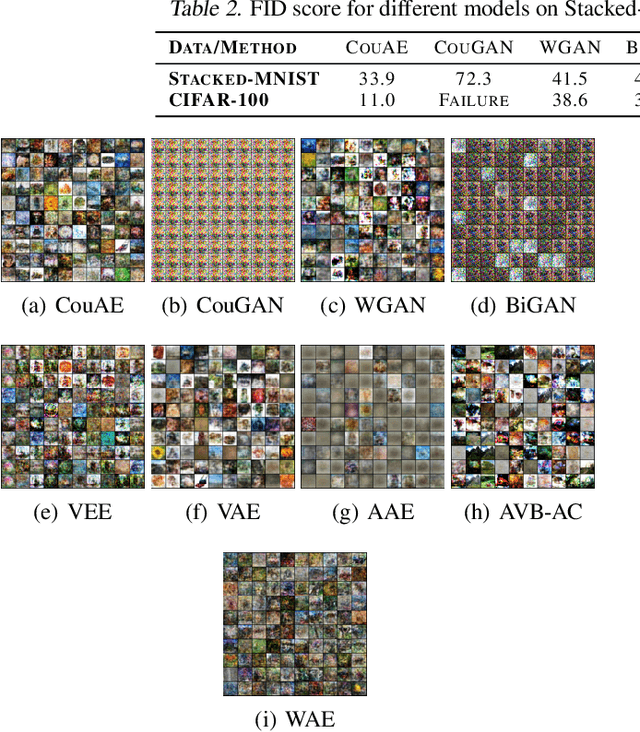
Estimating the true density in high-dimensional feature spaces is a well-known problem in machine learning. We propose a new implicit generative model based on autoencoders, whose training is guaranteed to converge to the global minimum of the objective function. This is achieved by using an appropriate family of kernel functions in the regularizer. Furthermore, we analyze the behaviour of the proposed model in the case of finite number of samples and provide an upper bound on the generalization error achieved by this global minimum. The theory is corroborated by extensive experimental comparisons on synthetic and real-world datasets against several approaches from the families of generative adversarial networks and autoencoder-based models.