Exploring Sparsity and Smoothness of Arbitrary $\ell_p$ Norms in Adversarial Attacks

Adversarial attacks against deep neural networks are commonly constructed under $\ell_p$ norm constraints, most often using $p=1$, $p=2$ or $p=\infty$, and potentially regularized for specific demands such as sparsity or smoothness. These choices are typically made without a systematic investigation of how the norm parameter \( p \) influences the structural and perceptual properties of adversarial perturbations. In this work, we study how the choice of \( p \) affects sparsity and smoothness of adversarial attacks generated under \( \ell_p \) norm constraints for values of $p \in [1,2]$. To enable a quantitative analysis, we adopt two established sparsity measures from the literature and introduce three smoothness measures. In particular, we propose a general framework for deriving smoothness measures based on smoothing operations and additionally introduce a smoothness measure based on first-order Taylor approximations. Using these measures, we conduct a comprehensive empirical evaluation across multiple real-world image datasets and a diverse set of model architectures, including both convolutional and transformer-based networks. We show that the choice of $\ell_1$ or $\ell_2$ is suboptimal in most cases and the optimal $p$ value is dependent on the specific task. In our experiments, using $\ell_p$ norms with $p\in [1.3, 1.5]$ yields the best trade-off between sparse and smooth attacks. These findings highlight the importance of principled norm selection when designing and evaluating adversarial attacks.

Perturbing the Phase: Analyzing Adversarial Robustness of Complex-Valued Neural Networks

Complex-valued neural networks (CVNNs) are rising in popularity for all kinds of applications. To safely use CVNNs in practice, analyzing their robustness against outliers is crucial. One well known technique to understand the behavior of deep neural networks is to investigate their behavior under adversarial attacks, which can be seen as worst case minimal perturbations. We design Phase Attacks, a kind of attack specifically targeting the phase information of complex-valued inputs. Additionally, we derive complex-valued versions of commonly used adversarial attacks. We show that in some scenarios CVNNs are more robust than RVNNs and that both are very susceptible to phase changes with the Phase Attacks decreasing the model performance more, than equally strong regular attacks, which can attack both phase and magnitude.

CVKAN: Complex-Valued Kolmogorov-Arnold Networks

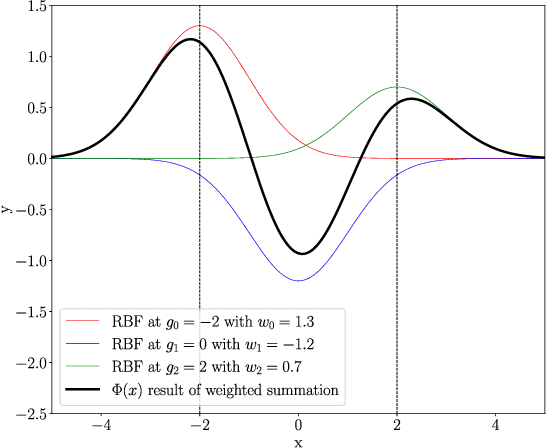
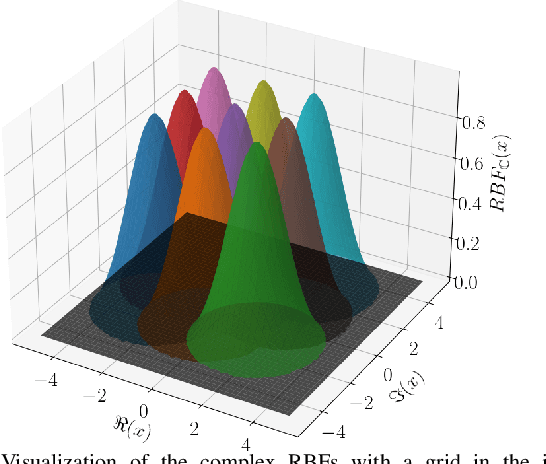
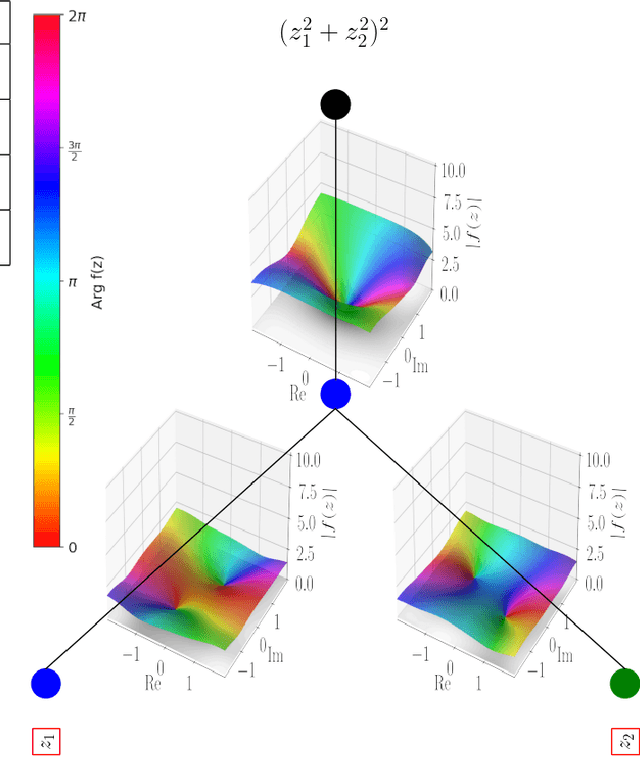
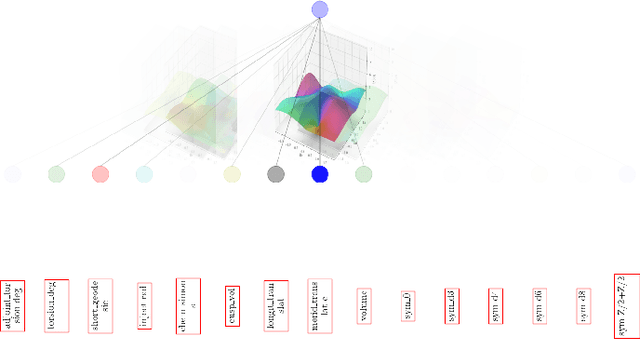
In this work we propose CKAN, a complex-valued KAN, to join the intrinsic interpretability of KANs and the advantages of Complex-Valued Neural Networks (CVNNs). We show how to transfer a KAN and the necessary associated mechanisms into the complex domain. To confirm that CKAN meets expectations we conduct experiments on symbolic complex-valued function fitting and physically meaningful formulae as well as on a more realistic dataset from knot theory. Our proposed CKAN is more stable and performs on par or better than real-valued KANs while requiring less parameters and a shallower network architecture, making it more explainable.

DeepCSHAP: Utilizing Shapley Values to Explain Deep Complex-Valued Neural Networks

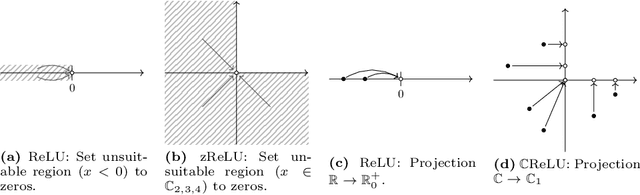
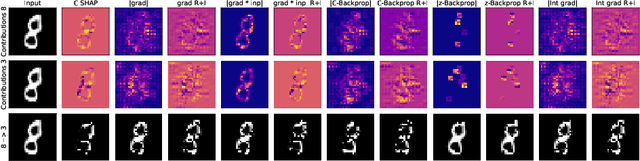
Deep Neural Networks are widely used in academy as well as corporate and public applications, including safety critical applications such as health care and autonomous driving. The ability to explain their output is critical for safety reasons as well as acceptance among applicants. A multitude of methods have been proposed to explain real-valued neural networks. Recently, complex-valued neural networks have emerged as a new class of neural networks dealing with complex-valued input data without the necessity of projecting them onto $\mathbb{R}^2$. This brings up the need to develop explanation algorithms for this kind of neural networks. In this paper we provide these developments. While we focus on adapting the widely used DeepSHAP algorithm to the complex domain, we also present versions of four gradient based explanation methods suitable for use in complex-valued neural networks. We evaluate the explanation quality of all presented algorithms and provide all of them as an open source library adaptable to most recent complex-valued neural network architectures.

Building Blocks for a Complex-Valued Transformer Architecture

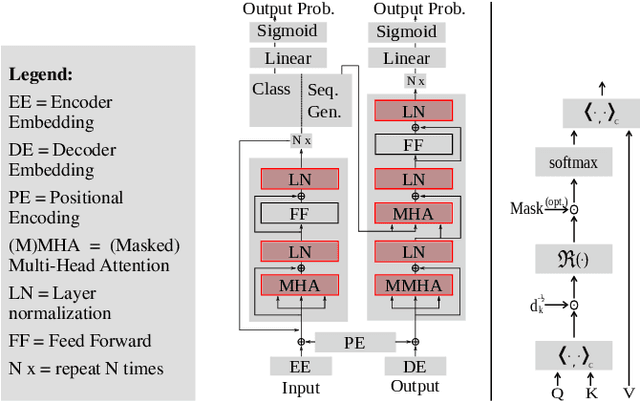
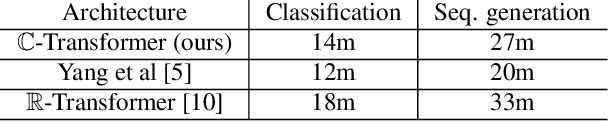
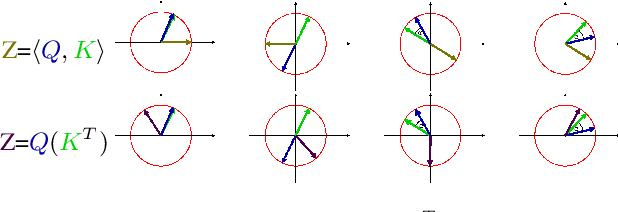
Most deep learning pipelines are built on real-valued operations to deal with real-valued inputs such as images, speech or music signals. However, a lot of applications naturally make use of complex-valued signals or images, such as MRI or remote sensing. Additionally the Fourier transform of signals is complex-valued and has numerous applications. We aim to make deep learning directly applicable to these complex-valued signals without using projections into $\mathbb{R}^2$. Thus we add to the recent developments of complex-valued neural networks by presenting building blocks to transfer the transformer architecture to the complex domain. We present multiple versions of a complex-valued Scaled Dot-Product Attention mechanism as well as a complex-valued layer normalization. We test on a classification and a sequence generation task on the MusicNet dataset and show improved robustness to overfitting while maintaining on-par performance when compared to the real-valued transformer architecture.

A Bhattacharyya Coefficient-Based Framework for Noise Model-Aware Random Walker Image Segmentation

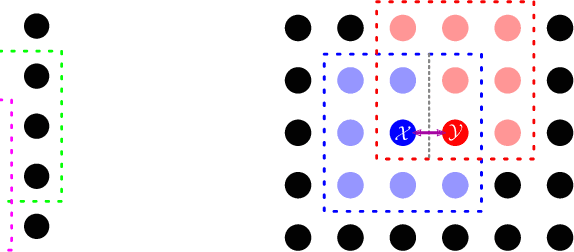
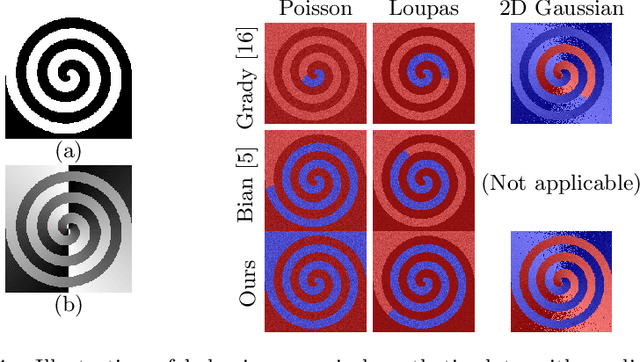
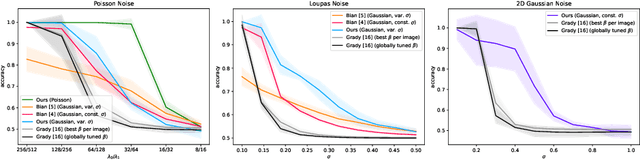
One well established method of interactive image segmentation is the random walker algorithm. Considerable research on this family of segmentation methods has been continuously conducted in recent years with numerous applications. These methods are common in using a simple Gaussian weight function which depends on a parameter that strongly influences the segmentation performance. In this work we propose a general framework of deriving weight functions based on probabilistic modeling. This framework can be concretized to cope with virtually any well-defined noise model. It eliminates the critical parameter and thus avoids time-consuming parameter search. We derive the specific weight functions for common noise types and show their superior performance on synthetic data as well as different biomedical image data (MRI images from the NYU fastMRI dataset, larvae images acquired with the FIM technique). Our framework can also be used in multiple other applications, e.g., the graph cut algorithm and its extensions.