On Using Deep Learning Proxies as Forward Models in Deep Learning Problems

Physics-based optimization problems are generally very time-consuming, especially due to the computational complexity associated with the forward model. Recent works have demonstrated that physics-modelling can be approximated with neural networks. However, there is always a certain degree of error associated with this learning, and we study this aspect in this paper. We demonstrate through experiments on popular mathematical benchmarks, that neural network approximations (NN-proxies) of such functions when plugged into the optimization framework, can lead to erroneous results. In particular, we study the behavior of particle swarm optimization and genetic algorithm methods and analyze their stability when coupled with NN-proxies. The correctness of the approximate model depends on the extent of sampling conducted in the parameter space, and through numerical experiments, we demonstrate that caution needs to be taken when constructing this landscape with neural networks. Further, the NN-proxies are hard to train for higher dimensional functions, and we present our insights for 4D and 10D problems. The error is higher for such cases, and we demonstrate that it is sensitive to the choice of the sampling scheme used to build the NN-proxy. The code is available at https://github.com/Fa-ti-ma/NN-proxy-in-optimization.

On the Robustness of 3D Object Detectors

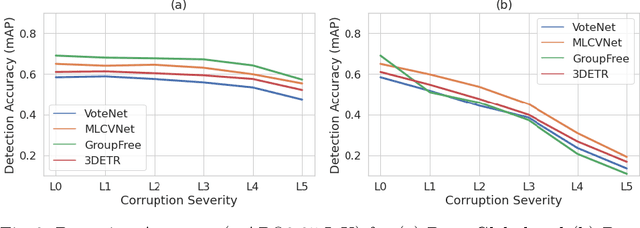
In recent years, significant progress has been achieved for 3D object detection on point clouds thanks to the advances in 3D data collection and deep learning techniques. Nevertheless, 3D scenes exhibit a lot of variations and are prone to sensor inaccuracies as well as information loss during pre-processing. Thus, it is crucial to design techniques that are robust against these variations. This requires a detailed analysis and understanding of the effect of such variations. This work aims to analyze and benchmark popular point-based 3D object detectors against several data corruptions. To the best of our knowledge, we are the first to investigate the robustness of point-based 3D object detectors. To this end, we design and evaluate corruptions that involve data addition, reduction, and alteration. We further study the robustness of different modules against local and global variations. Our experimental results reveal several intriguing findings. For instance, we show that methods that integrate Transformers at a patch or object level lead to increased robustness, compared to using Transformers at the point level.