Toward a language-theoretic foundation for planning and filtering

We address problems underlying the algorithmic question of automating the co-design of robot hardware in tandem with its apposite software. Specifically, we consider the impact that degradations of a robot's sensor and actuation suites may have on the ability of that robot to complete its tasks. We introduce a new formal structure that generalizes and consolidates a variety of well-known structures including many forms of plans, planning problems, and filters, into a single data structure called a procrustean graph, and give these graph structures semantics in terms of ideas based in formal language theory. We describe a collection of operations on procrustean graphs (both semantics-preserving and semantics-mutating), and show how a family of questions about the destructiveness of a change to the robot hardware can be answered by applying these operations. We also highlight the connections between this new approach and existing threads of research, including combinatorial filtering, Erdmann's strategy complexes, and hybrid automata.

Improper Filter Reduction

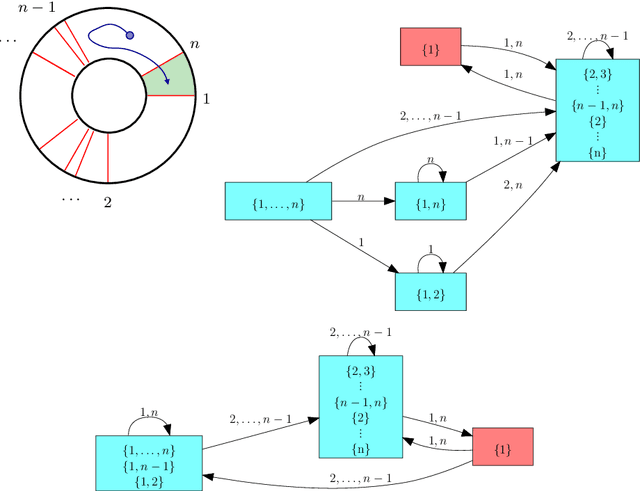
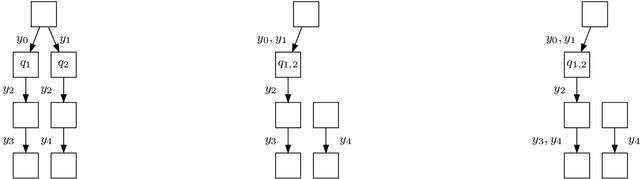
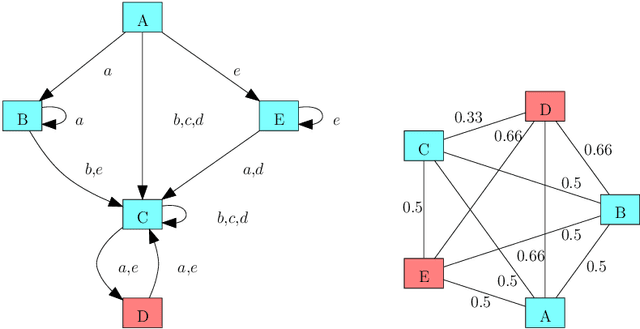
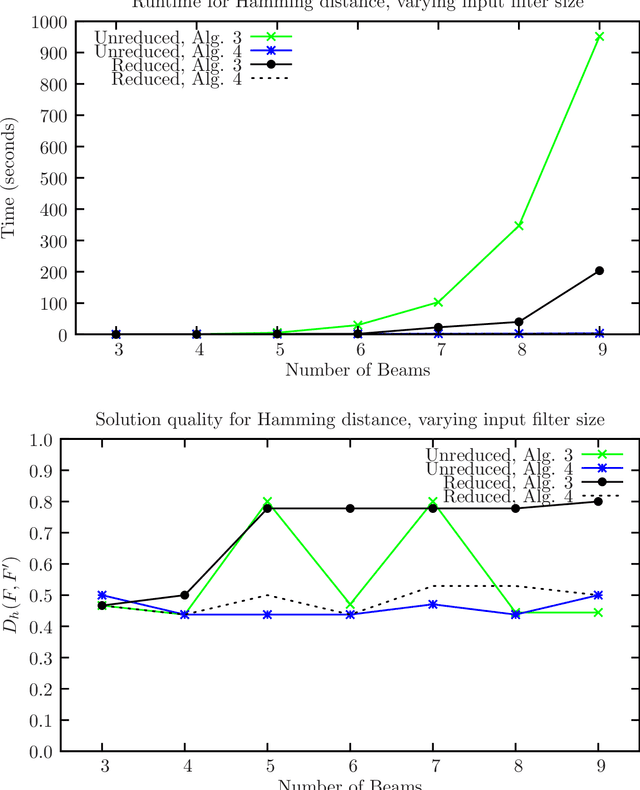
Combinatorial filters have been the subject of increasing interest from the robotics community in recent years. This paper considers automatic reduction of combinatorial filters to a given size, even if that reduction necessitates changes to the filter's behavior. We introduce an algorithmic problem called improper filter reduction, in which the input is a combinatorial filter F along with an integer k representing the target size. The output is another combinatorial filter F' with at most k states, such that the difference in behavior between F and F' is minimal. We present two metrics for measuring the distance between pairs of filters, describe dynamic programming algorithms for computing these distances, and show that improper filter reduction is NP-hard under these metrics. We then describe two heuristic algorithms for improper filter reduction, one greedy sequential approach, and one randomized global approach based on prior work on weighted improper graph coloring. We have implemented these algorithms and analyze the results of three sets of experiments.