Improper Filter Reduction
Paper and Code
Mar 01, 2017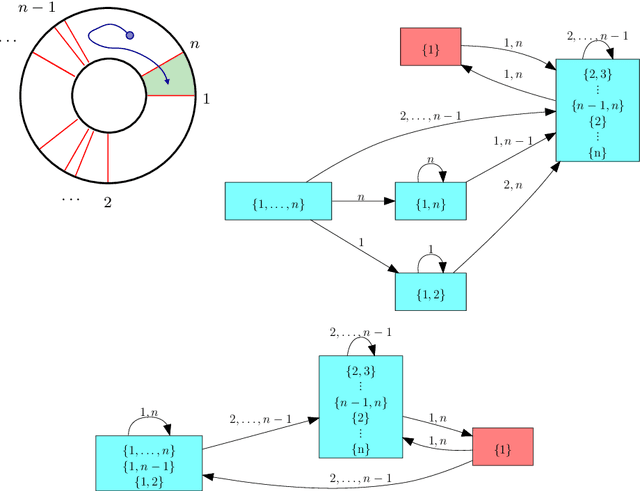
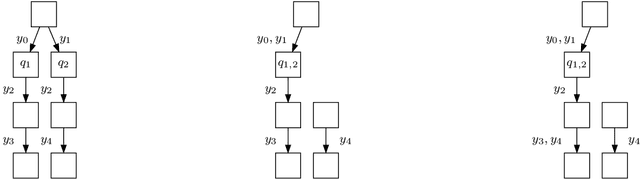
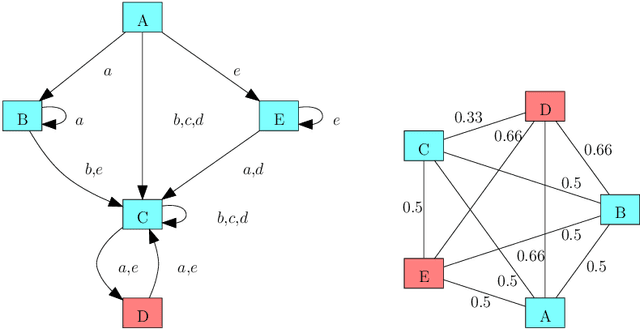
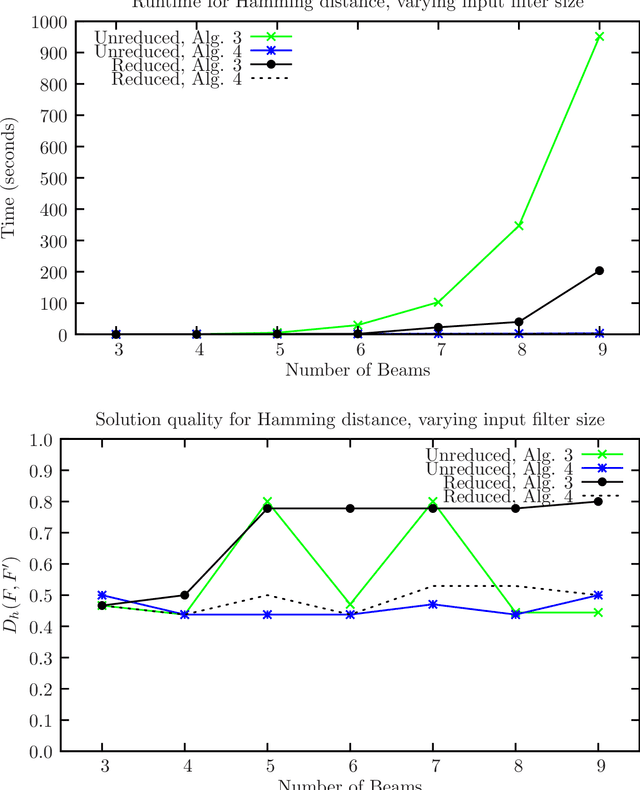
Combinatorial filters have been the subject of increasing interest from the robotics community in recent years. This paper considers automatic reduction of combinatorial filters to a given size, even if that reduction necessitates changes to the filter's behavior. We introduce an algorithmic problem called improper filter reduction, in which the input is a combinatorial filter F along with an integer k representing the target size. The output is another combinatorial filter F' with at most k states, such that the difference in behavior between F and F' is minimal. We present two metrics for measuring the distance between pairs of filters, describe dynamic programming algorithms for computing these distances, and show that improper filter reduction is NP-hard under these metrics. We then describe two heuristic algorithms for improper filter reduction, one greedy sequential approach, and one randomized global approach based on prior work on weighted improper graph coloring. We have implemented these algorithms and analyze the results of three sets of experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge