The Matrix Generalized Inverse Gaussian Distribution: Properties and Applications

While the Matrix Generalized Inverse Gaussian ($\mathcal{MGIG}$) distribution arises naturally in some settings as a distribution over symmetric positive semi-definite matrices, certain key properties of the distribution and effective ways of sampling from the distribution have not been carefully studied. In this paper, we show that the $\mathcal{MGIG}$ is unimodal, and the mode can be obtained by solving an Algebraic Riccati Equation (ARE) equation [7]. Based on the property, we propose an importance sampling method for the $\mathcal{MGIG}$ where the mode of the proposal distribution matches that of the target. The proposed sampling method is more efficient than existing approaches [32, 33], which use proposal distributions that may have the mode far from the $\mathcal{MGIG}$'s mode. Further, we illustrate that the the posterior distribution in latent factor models, such as probabilistic matrix factorization (PMF) [25], when marginalized over one latent factor has the $\mathcal{MGIG}$ distribution. The characterization leads to a novel Collapsed Monte Carlo (CMC) inference algorithm for such latent factor models. We illustrate that CMC has a lower log loss or perplexity than MCMC, and needs fewer samples.

Generalized Direct Change Estimation in Ising Model Structure

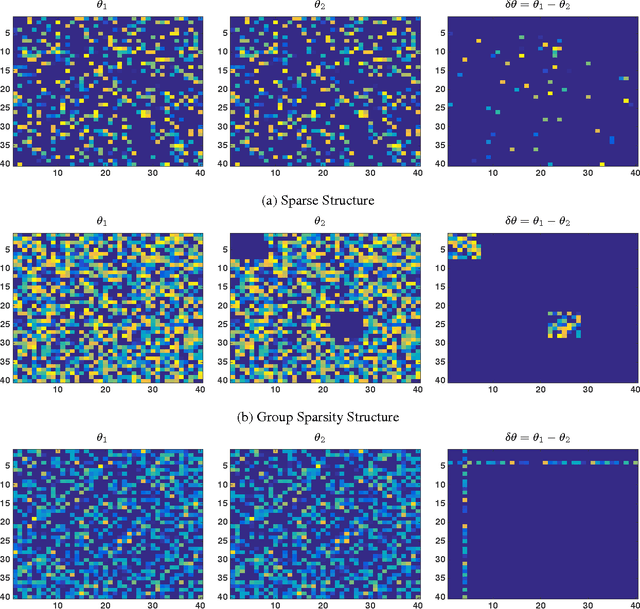
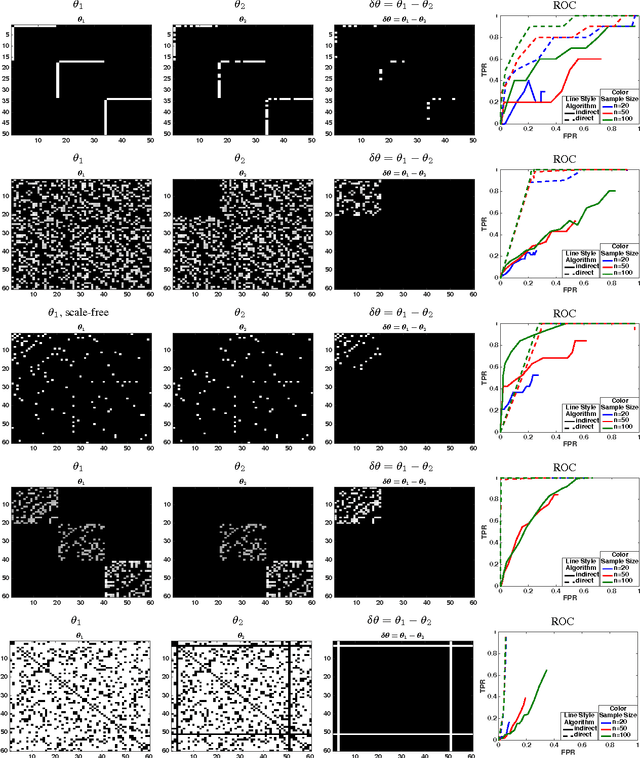
We consider the problem of estimating change in the dependency structure between two $p$-dimensional Ising models, based on respectively $n_1$ and $n_2$ samples drawn from the models. The change is assumed to be structured, e.g., sparse, block sparse, node-perturbed sparse, etc., such that it can be characterized by a suitable (atomic) norm. We present and analyze a norm-regularized estimator for directly estimating the change in structure, without having to estimate the structures of the individual Ising models. The estimator can work with any norm, and can be generalized to other graphical models under mild assumptions. We show that only one set of samples, say $n_2$, needs to satisfy the sample complexity requirement for the estimator to work, and the estimation error decreases as $\frac{c}{\sqrt{\min(n_1,n_2)}}$, where $c$ depends on the Gaussian width of the unit norm ball. For example, for $\ell_1$ norm applied to $s$-sparse change, the change can be accurately estimated with $\min(n_1,n_2)=O(s \log p)$ which is sharper than an existing result $n_1= O(s^2 \log p)$ and $n_2 = O(n_1^2)$. Experimental results illustrating the effectiveness of the proposed estimator are presented.

Estimation with Norm Regularization

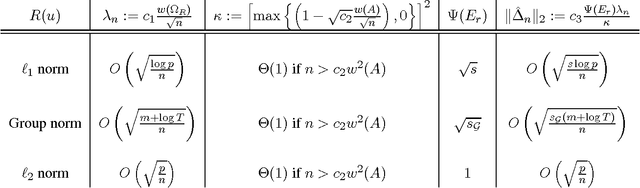
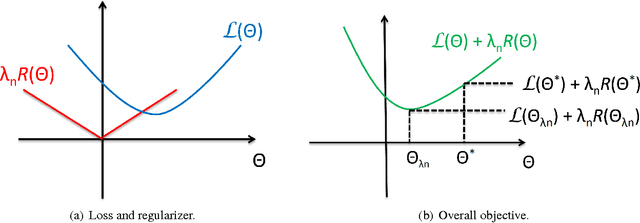
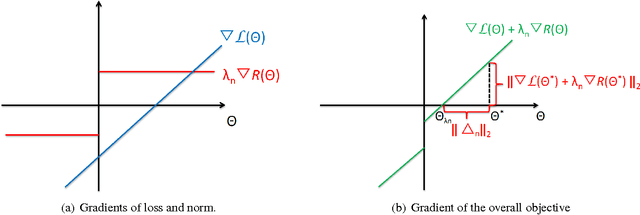
Analysis of non-asymptotic estimation error and structured statistical recovery based on norm regularized regression, such as Lasso, needs to consider four aspects: the norm, the loss function, the design matrix, and the noise model. This paper presents generalizations of such estimation error analysis on all four aspects compared to the existing literature. We characterize the restricted error set where the estimation error vector lies, establish relations between error sets for the constrained and regularized problems, and present an estimation error bound applicable to any norm. Precise characterizations of the bound is presented for isotropic as well as anisotropic subGaussian design matrices, subGaussian noise models, and convex loss functions, including least squares and generalized linear models. Generic chaining and associated results play an important role in the analysis. A key result from the analysis is that the sample complexity of all such estimators depends on the Gaussian width of a spherical cap corresponding to the restricted error set. Further, once the number of samples $n$ crosses the required sample complexity, the estimation error decreases as $\frac{c}{\sqrt{n}}$, where $c$ depends on the Gaussian width of the unit norm ball.