Estimation with Norm Regularization
Paper and Code
Nov 30, 2015
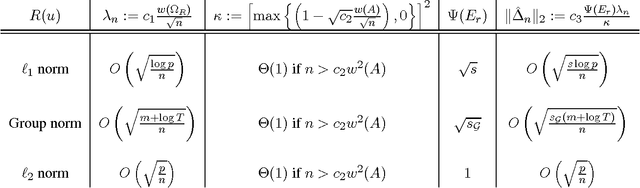
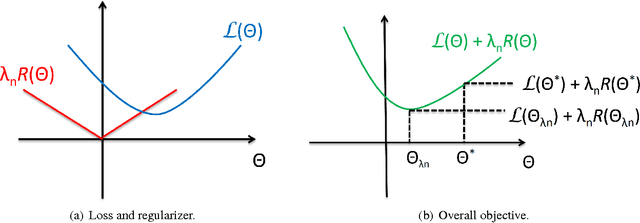
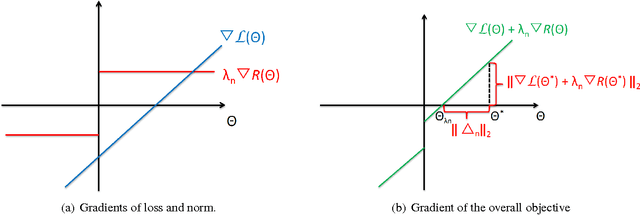
Analysis of non-asymptotic estimation error and structured statistical recovery based on norm regularized regression, such as Lasso, needs to consider four aspects: the norm, the loss function, the design matrix, and the noise model. This paper presents generalizations of such estimation error analysis on all four aspects compared to the existing literature. We characterize the restricted error set where the estimation error vector lies, establish relations between error sets for the constrained and regularized problems, and present an estimation error bound applicable to any norm. Precise characterizations of the bound is presented for isotropic as well as anisotropic subGaussian design matrices, subGaussian noise models, and convex loss functions, including least squares and generalized linear models. Generic chaining and associated results play an important role in the analysis. A key result from the analysis is that the sample complexity of all such estimators depends on the Gaussian width of a spherical cap corresponding to the restricted error set. Further, once the number of samples $n$ crosses the required sample complexity, the estimation error decreases as $\frac{c}{\sqrt{n}}$, where $c$ depends on the Gaussian width of the unit norm ball.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge