Generalized Direct Change Estimation in Ising Model Structure
Paper and Code
Jun 16, 2016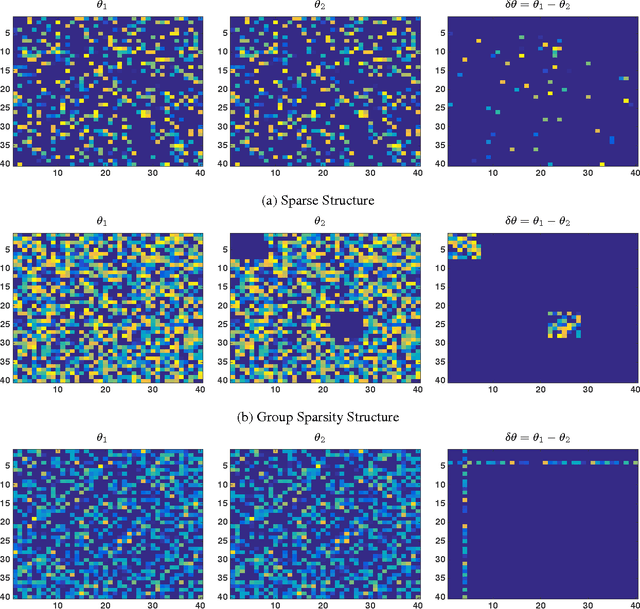
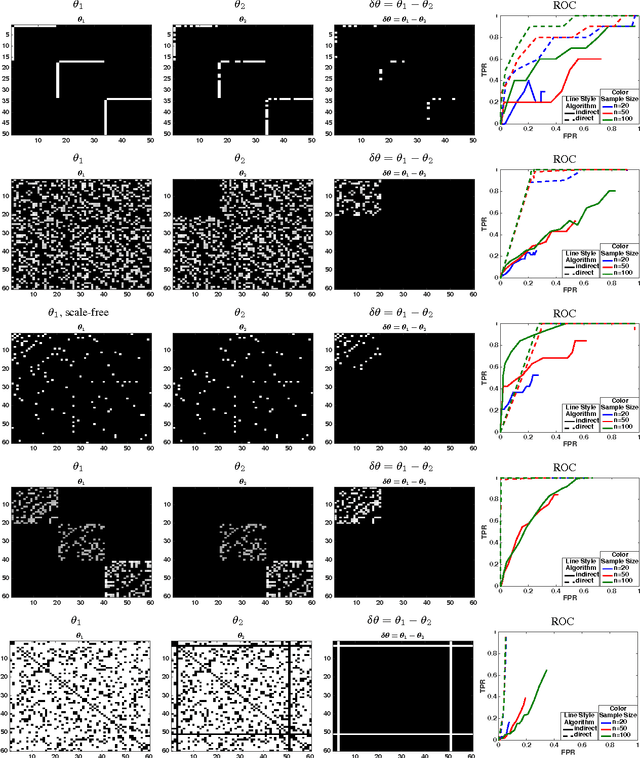
We consider the problem of estimating change in the dependency structure between two $p$-dimensional Ising models, based on respectively $n_1$ and $n_2$ samples drawn from the models. The change is assumed to be structured, e.g., sparse, block sparse, node-perturbed sparse, etc., such that it can be characterized by a suitable (atomic) norm. We present and analyze a norm-regularized estimator for directly estimating the change in structure, without having to estimate the structures of the individual Ising models. The estimator can work with any norm, and can be generalized to other graphical models under mild assumptions. We show that only one set of samples, say $n_2$, needs to satisfy the sample complexity requirement for the estimator to work, and the estimation error decreases as $\frac{c}{\sqrt{\min(n_1,n_2)}}$, where $c$ depends on the Gaussian width of the unit norm ball. For example, for $\ell_1$ norm applied to $s$-sparse change, the change can be accurately estimated with $\min(n_1,n_2)=O(s \log p)$ which is sharper than an existing result $n_1= O(s^2 \log p)$ and $n_2 = O(n_1^2)$. Experimental results illustrating the effectiveness of the proposed estimator are presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge